Регуляризация дифференцирования

При численном дифференцировании приходится вычитать друг из друга близкие значения функции. Это приводит к уничтожению первых значащих цифр, т.е. потере части достоверных знаков числа. Если значения функции известны с малой точностью, то встает вопрос: останется ли в разности хоть один верный знак?

Исследуем ошибки численного дифференцирования. Мы получили (формула (1)), что при интерполировании алгебраическим многочленом производная n -го порядка определяется формулой типа

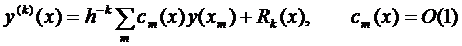(3)

Если формула имеет точность порядка p, то это означает, что ее остаточный член 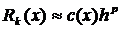. Этот остаточный член определяет погрешность метода и неограниченно убывает при h →0.

Но есть еще неустранимая погрешность, связанная с погрешностью заданной функции δ y (x). Поскольку точный вид этой погрешности неизвестен, можно оценить только мажоранту неустранимой погрешности 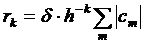; она неограниченно возрастает при h →0. Фактически неустранимая погрешность нерегулярно зависит от величины шага, беспорядочно осциллируя в границах, определенных мажорантой. Пока шаг достаточно велик, при его убывании неустранимая погрешность мала по сравнению с погрешностью метода, поэтому полная погрешность убывает. При дальнейшем уменьшении шага неустранимая погрешность становится заметной, что появляется в не вполне регулярной зависимости результатов вычислений от величины шага. Наконец, при достаточно малом шаге неустранимая погрешность становится преобладающей, и при дальнейшем уменьшении шага результат становится все менее достоверным. Полная погрешность мажорируется суммой R_k+r_k. Оптимальным будет шаг, соответствующий минимуму этой кривой. Можно показать, что

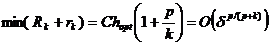
Меньший шаг невыгоден, а меньшая погрешность, вообще говоря, недостижима (хотя отдельные вычисления случайно могут оказаться более точными, мы об этом не сможем узнать). Эта минимальная ошибка тем меньше, чем меньше погрешность входных данных и порядок вычисляемой производной и чем выше порядок точности формулы.

При δ y (x) →0 можно получить сколь угодно высокую точность результата, если шаг h стремится к нулю, будучи всегда не менее h_opt (δ) (h ≥ h_opt (δ)). Но если допустить h < h_opt (δ), то результат предельного перехода может оказаться неправильным.

Эта тонкость связана с некорректностью задачи численного дифференцирования. Пусть погрешность входных данных . Она приводит к погрешности первой производной 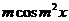. При m →∞ погрешность функции в чебышевской норме 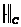неограниченно убывает, а погрешность производной в той же норме неограниченно растет , если функция x (t) задана на любом конечном отрезке). Таким образом, нет непрерывной зависимости производной от функции, т.е. операция численного дифференцирования некорректна. Особенно сильно это сказывается при вычислении производных высокого порядка.

Изложенный выше способ определения оптимального шага и запрещение вести расчет с шагом меньше оптимального есть способ регуляризации численного дифференцирования, называемый регуляризацией по шагу.

Не нашли, что искали? Воспользуйтесь поиском: