Л9 Классификация и общая характеристика методов решения дифференциальных уравнений. Хорошо и плохо обусловленные задачи

Уравнения, в которых неизвестные функции входят под знак производной, называют дифференциальными. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Дифференциальным уравнением с частными производными называется уравнение, включающее, по меньшей мере, одну частную производную от неизвестной функции двух или более независимых переменных.

Обыкновенным дифференциальным уравнением порядка n называется уравнение

,

которое связывает независимую переменную x, искомую функцию y=y(x) и ее производные . Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка

(1)

Обыкновенными дифференциальными уравнениями можно описать задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, сопротивления материалов (например, статический прогиб упругого стержня) и многие другие. Ряд важных задач для уравнений в частных производных также сводится к задачам для обыкновенных дифференциальных уравнений.

К уравнениям в частных производных приводят задачи газовой динамики, теплопроводности, переноса излучения, распространения нейтронов, теории упругости, электромагнитных полей, процессов переноса в газах, квантовой механики и многие другие.

Дифференциальное уравнение, как обыкновенное, так и с частными производными, имеет в общем случае бесчисленное множество решений. Поэтому, если физический процесс описывается с помощью дифференциального уравнения, то для однозначной характеристики этого процесса к уравнению нужно присоединить какие-то дополнительные данные. Эти дополнительные данные в простейшем случае состоят из начальных и краевых (граничных) условий. В сущности, различить эти условия можно лишь в том случае, когда одна из независимых переменных играет роль времени, а другая – пространственной координаты (для случая двух независимых переменных). При этом условия, относящиеся к начальному моменту времени, называются начальными, а условия, относящиеся к фиксированным значениям координат (обычно это координаты граничных точек рассматриваемого линейного континуума), - краевыми. Решение требуется найти в некоторой области изменения независимых переменных G(t, x ,…). Полная математическая постановка задачи содержит дифференциальное уравнение, а также дополнительные условия, позволяющие выделить единственное решение среди семейства решений этого уравнения. Дополнительные условия задаются обычно на границе области G.

Основной задачей, относящейся к уравнению (1), является задача Коши: найти решение уравнения (1)

, (2)

удовлетворяющее начальному условию

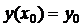. (3)

Иными словами, требуется найти интегральную кривую (2), проходящую через заданную точку 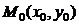Достаточные условия существования и единственности решения задачи Коши (1), (3) дает

Теорема Пикара. Пусть функция непрерывна в прямоугольнике 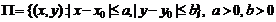и удовлетворяет условию Липшица по y равномерно относительно x, т.е. для всех x, и , , . Пусть , . Тогда задача Коши (1), (3) на промежутке имеет единственное решение .

Здесь N - некоторая постоянная (константа Липшица), зависящая, в общем случае, от a и b

Уравнение , (4)

где x - независимая переменная, y - искомая функция, а функция F определена и непрерывна в некоторой области 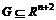() и во всяком случае зависит от , называется обыкновенным дифференциальным уравнением n -го порядка.

Дифференциальное уравнение n -го порядка, разрешенное относительно старшей производной, имеет вид

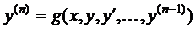, (5)

где функция g также предполагается непрерывной в некоторой области изменения своих аргументов.

Решением уравнения (5) на интервале 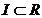называется функция , удовлетворяющая условиям: 1) y (x) непрерывно дифференцируема n раз на I;

2) ;

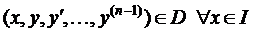3) обращает уравнение (5) в тождество, т.е.

. Аналогично определяется решение задачи (4).

Задачей Коши (или начальной задачей) для уравнения (5) называется задача нахождения решения уравнения (5), удовлетворяющего начальным условиям

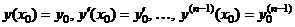(6)

где 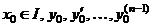- заданные числа.

Существование и единственность решения задачи Коши гарантирует следующая

Теорема Коши-Пикара. Если функция непрерывна в области и удовлетворяет условию Липшица по переменным , то для любой точки существует единственное решение уравнения (5), определенное в некоторой окрестности точки и удовлетворяющее условиям (6).

В приложениях часто встречаются системы обыкновенных дифференциальных уравнений. Система дифференциальных уравнений

(7)

называется системой в нормальной форме или системой, разрешенной относительно производных от неизвестных функций .

Решением системы уравнений (7) на промежутке называется совокупность непрерывно дифференцируемых на функций , , 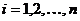которая, будучи подставлена в уравнения (7), обращает их в тождества

для всех .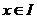

Воспользовавшись векторными обозначениями

, ,

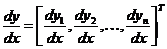систему уравнений (7) можно записать в векторной форме:

, (8)

где - заданная вектор-функция.

Так как система дифференциальных уравнений имеет бесчисленное множество решений, то для выделения одного конкретного решения , кроме уравнения, нужны дополнительные условия. Задание начальных условий

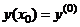(9)

приводит к задаче Коши для системы обыкновенных дифференциальных уравнений.

Гарантия однозначной разрешимости задачи Коши дается приведенными ниже достаточными условиями.

Теорема существования и единственности решения. Пусть в некоторой окрестности начальных значений система (8) обладает следующими свойствами:

1) правые части 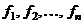определены и непрерывны в ;

2) функции 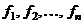в окрестности удовлетворяют условиям Липшица по зависимым переменным , т.е.

, где , и - некоторая постоянная (константа Липшица). Тогда существует единственное решение системы (8), определенное в некоторой окрестности и удовлетворяющее заданным начальным условиям (9).

Систему, содержащую производные высших порядков и разрешенную относительно старших производных искомых функций, можно привести к виду (8) путем введения новых неизвестных функций. В частности, для дифференциального уравнения -го порядка

, (10)

полагая будем иметь эквивалентную нормальную систему

(11)

Методы решения делятся на точные, приближенные аналитические и численные.

К точным относятся методы, позволяющие выразить решение дифференциального уравнения через элементарные функции либо представить его при помощи квадратур от элементарных функций. Нахождение точного общего решения дифференциального уравнения облегчает качественное исследование этого решения и его дальнейшую обработку. Однако классы уравнений, для которых разработаны методы получения точных решений, сравнительно узки и охватывают лишь малую часть возникающих на практике задач. Например, доказано, что решение уравнения 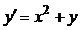не выражается через элементарные функции, а уравнение

можно точно проинтегрировать и найти общее решение:

.

Однако для вычисления конкретного значения надо численно решить трансцендентное уравнение, таким образом, задача сводится к не менее сложной.

Приближенными аналитическими будем называть методы, в которых решение получается как предел некоторой последовательности 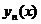, где 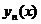выражаются через элементарные функции или с помощью квадратур. Ограничиваясь конечным числом n, получаем приближенное выражение для .

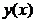Численные методы – это алгоритмы вычисления приближенных значений искомого решения на некоторой выбранной конечной сетке аргументов. Решение при этом получается в виде таблицы.

Приближенные аналитические и численные методы не позволяют найти общего решения дифференциального уравнения, они могут дать только какое-то частное решение. Это их основной недостаток. Зато эти методы применимы к очень широким классам уравнений и всем типам задач для них. Поэтому с появлением быстродействующей вычислительной техники эти методы стали основным способом решения конкретных практических задач.

Численные методы можно применять только к корректно поставленным (или регуляризованным) задачам. Однако для успешного применения численных методов формального выполнения условий корректности может оказаться недостаточным. Надо, чтобы задача была хорошо обусловленной (устойчивой), т.е. малые изменения исходных данных приводили бы к малым изменениям результатов. Если это условие не выполнено, т.е. задача плохо обусловлена (слабо устойчива), то небольшие изменения исходных данных или эквивалентные им вычислительные погрешности могут сильно исказить и совершенно обесценить решение.

В качестве примера плохой обусловленности рассмотрим задачу:

Общее решение имеет вид , из начального условия находим С =0, следовательно, .

Изменим начальное условие: . Тогда С =10^-6 и , т.е. решение изменилось очень сильно.

При дальнейшем изложении будем предполагать, не оговаривая этого каждый раз, что для рассматриваемых дифференциальных уравнений выполнены условия существования и единственности решений. Для простоты записи при решении задачи Коши мы всюду ограничимся случаем одного уравнения первого порядка. Алгоритмы для случая системы уравнений легко получаются из алгоритмов, составленных для одного уравнения, формальной заменой и на и .

Не нашли, что искали? Воспользуйтесь поиском: