Оценка погрешности квадратурных формул

Так как при получении формул Ньютона-Котеса мы используем равенство

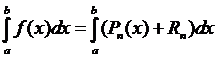
где P_n (x) интерполяционный полином степени n, а R_n – его погрешность, то погрешность соответствующей квадратурной формулы равна . Явное выражение для погрешности интерполяционного полинома было получено ранее. Отсюда получаются формулы для оценки погрешности обобщенной формулы трапеций

(8)

и обобщенной формулы Симпсона

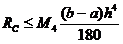(9)

где .

Однако на практике часто оказывается сложным оценить вторую и, тем более, четвертую производные подынтегральной функции. Поэтому применяется принцип Рунге оценки погрешностей квадратурных формул. Изложим его применительно к формуле Симпсона. Введем обозначения: I_k - приближенное значение искомого интеграла, вычисленное по формуле Симпсона (7) при разбиении отрезка интегрирования на k частей c шагом h =(b - a)/ k; R_k – его погрешность; I _{2 k} – значение, вычисленное по той же формуле при разбиении отрезка интегрирования на 2 k частей c шагом h /2с погрешностью R _{2 k}. Тогда из формулы (9) получаем: , следовательно, R_k =16 R _{2 k}. R_k = I – I_k, где I – точное значение искомого интеграла, а R _{2 k} = I – I _{2 k}. Таким образом, I = I_k + R_k и I = I _{2 k} + R _{2 k}, приравнивая правые части этих выражений, получаем I_k +16 R _{2 k} = I _{2 k} + R _{2 k}, отсюда

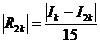. (10)

Применение принципа Рунге для оценки погрешности обобщенной формулы трапеций аналогичным образом дает

(11)

Принцип Рунге оценки погрешности по-другому называется способом двойного счета для оценки погрешности и широко применяется на практике при решении различных задач. При этом для оценки погрешности полученного результата один и тот же расчет оказывается необходимым применить дважды на двух разных сетках, шаги которых различаются ровно в два раза.

Для того чтобы использовать принцип Рунге для вычисления интеграла с заранее заданной точностью, поступают следующим образом. Выбирают некоторое начальное значение k (например, k =2), составляют таблицу значений подынтегральной функции в k +1 точках и вычисляют значение интеграла по той или иной квадратурной формуле. Затем значение k удваивают (k:= 2 k) и снова вычисляют значение интеграла. Затем, применяя формулы (10) или (11), оценивают погрешность полученного результата. Если эта погрешность оказывается меньшей заданной точности, искомое значение интеграла найдено. В противном случае вычисления продолжаются: число k снова удваивается, вычисляется новое значение интеграла, оценивается его погрешность и т.д. При этом для оценки погрешности используется новое и предыдущее значения интеграла.

Не нашли, что искали? Воспользуйтесь поиском: