Комбинированный метод

Пусть корень ξ уравнения

(1)

отделен на отрезке [ a,b ], причем и непрерывны и сохраняют определенные знаки при . Соединяя способ пропорциональных частей и метод Ньютона, получаем метод, на каждом шаге которого находим приближенные значения по недостатку x_n и избытку для корня 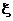. Отсюда, в частности, вытекает, что цифры, общие для x_n и , обязательно принадлежат точному корню 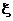. Теоретически здесь возможны четыре случая:

	>0	>0
	>0	<0
	<0	>0
	<0	<0

Мы ограничимся разбором лишь первого случая. Остальные рассматриваются аналогично, кроме того, их легко свести к первому, если заменить рассматриваемое уравнение эквивалентными ему: – f (x) = 0 или ± f (– z) = 0, где z = – x.

Итак, >0, >0 при . Полагаем x ₀= a, = b и получаем вычислительную схему комбинированного метода, которая имеет вид:

(10)

Заметим, что на каждом шаге метод хорд применяется к новому отрезку[ x_n, ].

Из доказанного выше (при изложении методов хорд и касательных) следует, что

x_n < ξ< и 0< ξ- x_n < - x_n (11)

Если допустимая погрешность приближенного корня задана заранее и равна ε, то процесс вычислений прекращается при выполнении условия - x_n < ε.

Метод простой итерации.

Этот метод заключается в следующем. Пусть дано уравнение (1), где f (x) – непрерывная функция, и требуется определить его корни. Заменим уравнение (1) равносильным:

x = φ (x) (2)

Выберем x ₀ и вычислим x ₁=φ(x ₀), x ₂=φ(x ₁) и т.д. Продолжая этот процесс, получим последовательность чисел

(3)

Если эта последовательность сходящаяся, т.е. существует предел , то, переходя к пределу в формуле (3) и предполагая функцию φ(x) непрерывной, получаем или ξ= φ(ξ). Таким образом, предел ξ является корнем уравнения(1) и может быть вычислен по формуле (3) с любой степенью точности.

Процесс итераций (3) может быть и расходящимся, поэтому для практического применения нужно выяснить достаточные условия сходимости итерационного процесса.

Теорема 4. Пусть функция φ(x) определена и дифференцируема на отрезке [ a, b ], причем все ее значения при . Тогда, если существует правильная дробь q такая, что

при (4)

то 1) процесс итерации (3) сходится независимо от начального приближения ;

2) предельное значение - единственный корень уравнения (2) на отрезке [ a, b ].

Доказательство. Рассмотрим два последовательные приближения и . Рассмотрим их разность . Применяя теорему Лагранжа, будем иметь: , где . Следовательно, используя (4), получаем

(5)

При n=1, 2, … последовательно получаем

… … …...

(6)

Рассмотрим ряд:

x ₀+(x ₁- x ₀)+(x ₂- x ₁)+…+(x_n - x_{n -1})+…, (7)

для которого приближения x_n являются частичными суммами, т.е. x_n = s_{n +1}.

В силу неравенств (6) члены ряда (7) меньше соответствующих членов геометрической прогрессии со знаменателем q <1, поэтому ряд (7) сходится, притом абсолютно. Следовательно, существует предел , причем . Переходя к пределу в равенстве (3), в силу непрерывности функции φ(x) получаем ξ= φ(ξ). (8)

Таким образом, ξ – корень уравнения (2), а следовательно, и (1). Другого корня на отрезке [ a, b ] уравнение(2) не имеет. Действительно, если

ζ= φ(ζ), (9)

то из равенств (8) и (9) и теоремы Лагранжа получим . Отсюда и ξ- ζ=0, следовательно, ξ= ζ и корень единственный.

Не нашли, что искали? Воспользуйтесь поиском: