
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Арапайым пішіндерді сингониялар бойынша шолу
Табиғатта кристалдар 47 қарапайым пішіндер түрінде кездеседі. Әрбір сингония кристалдарына өздерінің белгілі бір қарапайым пішіндері тән. Қарапайым пішіндердің аттары грек тілінен шыққан. Грекше моно – бір, ди –екі, три – үш, тетра – төрт, пента – бес, гекса – алты, окта – сегіз, дека – он, додека – он екі, эдра – жақ, пинакс – тақтай, скаленос – қисық, трапеца – үстел, гониа – бұрыш, клинос – еңкіш.
Триклиндік сингония деп аталу себебі, оның қарапайым пішіндерінің кристаллографиялық үш өсінің үшеуі де бір-біріне тік емес, еңкіш келеді (грекше «три» – «үш», «клин» – «еңкейту»). Мысалы, бұл сингонияға кіретін минералдар – плагиоклаздар, микроклин және т.б.
Моноклиндік сингония деп аталу себебі, мұның бір ғана өсі еңкіш келеді (грекше «моно» – «бір», «клин» – «еңкейту»), басқа екі өсі тік болады. Мысалы, ортоклаз, авгит, гипс.
Ромбылық сингонияға жататын кристалдардың көлденең қимасының пішіні көбінесе ромб түрінде болады. Мысалы, оливин, сурьма, барит.
Тетрагондық сингония жататын кристалдардың көлденең қимасы тең төрт бұрышты – шаршы болады. Мысалы, циркон.
Тригондық сингонияда кристалдың көлденең қимасы тең үшбұрыштық. Мысалы, кварц, кальцит.
Гексагондық сингонияда – алты бұрышты, яғни алты дәрежелі симметрия өсі бар кристалдар осыған жатады. Мысалы, апатит, нефелин, берилл.
Кубтық сингония деп аталуы, оның атынан ақ түсінікті. Осы кубтық сингонияда симметриялық мүшелері ең көп. Мысалы, ас тұзы, алмаз, анартастар, пирит.
Симметриялардың әрқайсысына тән қарапайым пішіндерді сингониялары бойынша шолып танысайық.
Төменгі сингонияларының қарапайым пішіндері: моноэдр – бір жақтан тұратын қарапайым пішін; пинакоид – екі тең және параллель жақтар, олар кейде теріс орналасқан болады; диэдр – екі тең қиылысатын жақтар (олар өздерінің жалғасында қиылысуы мүмкін);ромбылық призма – төрт тең және қосақтанған параллель жақтардан тұрады, ал қимасында ромб болады; ромбылық пирамида – төрт тең үшбұрышты және бір төбеде шатыр сияқты қиылысқан жақтар, кимасында ромб. Осы аталған пішіндер ашық деп саналады, өйткені олар кеңістікті қауыстырмайды. Ромбылық призма ашық пішін, әдетте оны қауыстыратын пинакоид барлығын көрсетеді.
Төменгі сингонияларының жабық пішіндері (...7 суретке сәйкес): ромбылық дипирамида – табандарымен біріккен екі ромбылық пирамида, көлденең кимасында ромб; ромбылық тетраэдр – төрт жағы, кеңістікті қауыстырады және олардың пішіндері қиғаш үш бұрыштар болады.
Осы аталған пішіндер кубтық сингонияда кездеспейді, бірақ моноэдр және пинакоид орта категориядағы кристалдарда кездесуі мүмкін. Бұлардың сырт пішіндері пирамидалар, дипирамидалар және призмалар. Бұдан басқа скланоэдрлар, трапецоэдрлар және ромбоэдрлар кездесуі мүмкін.
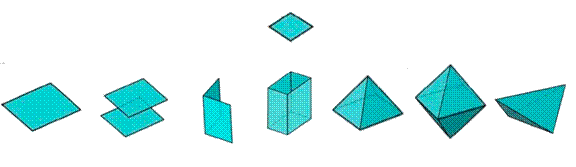
1) а б 2) а б 3) а б в
1) триклиндік сингониясының қарапайым пішіндері: а) моноэдр, б) пинакоид; 2) моноклиндік сингониясының – а) диэдр, б) ромбылық призма; 3) ромбылық сингониясының – а) ромбылық пирамида, б) ромбылық дипирамида, в) ромбылық тетраэдр.
7 сурет – Төменгі сингонияларының қарапайым пішіндері
Ортаңғы категорияның тригондық сингониясына келесі қарапайым пішіндер тән: тригодық призма, тригондық пирамида, тригондық оң трапецоэдр, тригондық сол трапецоэдр, тригондық дипирамида, дитригондық призма, дитригондық пирамида, тригондық скаленоэдр, ромбоэдр, дитригондық дипирамида (...8 суретке сәйкес). Ортаңғы категорияға тән 25 қарапайым пішіндері жоғарғы және төменгі категориялы сингониялардың ешқайсында кездеспейді.


1 2 3 4 5



6 7 8 9 10
1) тригодық призма, 2) тригондық пирамида, 3) оң тригондық трапецоэдр, 4) сол тригондық трапецоэдр, 5) тригондық дипирамида, 6) дитригондық призма, 7) дитригондық пирамида, 8) тригондық скаленоэдр, 9) ромбоэдр, 10) дитригондық дипирамида.
8 сурет – Ортанғы категорияның тригондық сингониясының қарапайым пішіндері
Ортаңғы категорияның тетрагондық сингониясына келесі қарапайым пішіндер тән: тетрагондық призма, тетрагондық пирамида, тетрагондық дипирамида, тетрагондық тетраэдр, тетрагондық трапецоэдр, дитетрагондық призма, дитетрагондық пирамида, дитетрагондық дипирамида, тетрагондық скаленоэдр (...9 суретке сәйкес).


1 2 3 4 5
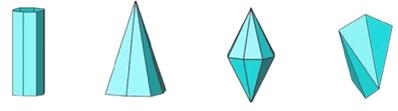
6 7 8 9
1) тетрагондық призма, 2) тетрагондық пирамида, 3) тетрагондық дипирамида, 4) тетрагондық тетраэдр, 5) тетргагондық трапецоэдр, 6) дитетрагондық призма, 7) дитетрагондық пирамида, 8) дитетрагондық дипирамида, 9) тетрагондық скаленоэдр.
9 сурет – Ортанғы категорияның, тетрагондық сингониясының қарапайым пішіндері
Ортаңғы категорияның гексагондық сингониясына келесі қарапайым пішіндер тән: гексагондық призма, гексагондық пирамида, гексагондық дипирамида, гексагондық трапецоэдр, дигексагондық призма, дигексагондық пирамида, дигексагондық дипирамида (...10 суретке сәйкес).
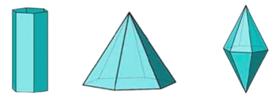


1 2 3 4 5 6 7
1) гексагондық призма, 2) гексагондық пирамида, 3) гексагондық дипирамида, 4) гексагондық трапецоэдр, 5) дигексагондық призма, 6) дигексагондық пирамида, 7) дигексагондық дипирамида.
10 сурет – Ортанғы категориясының, гексагондық сингониясының қарапайым пішіндері
Ортаңғы сингонияларда, төменгі категорияның қарапайым пішіндерінен, моноэдр және пинакоид кездеседі. Ашық пішіндері боп призмалар және пирамидалар саналады. Сәйкес сингонияларында тригондық, тетрагондық және гексагондық призмалар кездеседі. Жоғарғы ретті L3, L4, немесе L6 өстеріне перпендикуляр қималарының пішіндері үшбұрышты, шаршы немесе алты бұрышты. Дипирамидалар, скаленоэдрлер, трапецоэдрлер, ромбоэдрлер және тетрагондық тетраэдр жабық пішіндерге жатады.
Дипирамидалар тригондық, тетрагондық және гексагондық болады. Скаленоэдр – ол жақтары әр түрлі қабырғалы үшбұрыштардан туратың қарапайым пішін. Скаленоэдрлер тек тригондық және тетрагондақ сингонияларда кездеседі. Трапецоэдр дипирамидаға ұқсас, осы қарапайым пішіннің жақтары төрт бұрыштардан тұрады, ал бүйір қабырғалары бір жазықтықта жатпайды. Трапецоэдрлар тек симметрия жазықтары жоқ симметрияның үш түрінде болуы мүмкін. Ромбоэдр – оның алты жақтары ромбыдан тұрады, ол диагональдары бойынша созылған немесе қысылған текшеге ұқсас. Ол тек тригондық және гексагондық сингонияларға тән. Тетрагондық тетраэдр – оның төрт тең жақтары, бүйірлері тең үшбұрыштардан тұрады.
Кубтық сингонияға 15 қарапайым пішін жатады, олардың бәрі жабық пішіндер болады. Төменгі және ортаңғы сингониялардың қарапайым пішіндері кездеспейді. Куб (гексаэдр) алты қос-қостаған параллельді шаршы жақтардан тұрады. Ал текшенің әр жағын төрт тең үшбұрыштарымен ауыстырса, сонда тетрагексаэдр пайда болады. Октаэдр сегіз қос-қостаған параллель тең үшбұрыштардан тұрады. Кубтық сингонияның тетраэдрі төрт тең жақты үшбұрыштан тұрады, олар кеңістікті қауыстырады.
Жоғарғы категориядағы кубтық сингониясына тән қарапайым пішіндері: тетраэдрден шыққан пішіндер – тригонтритетраэдр (12 жақты фигура, жақтары ұшбұрыштар), тетрагонтритетраэдр (12 жағы – төрт бұрыштар), пентагонтритетраэдр (12 жағы – бес бұрыштар), гексатертраэдр (24 жағы – үшбұрыштар); октаэдрден шыққан пішіндер – тригонтриоктаэдр (24 жағы – үшбұрыштар), тетрагонтриоктаэдр (24 жағы – төрт бұрыштар), пентагонтриоктаэдр (24 жағы – бес бұрыштар), гексаоктаэдр (48 жағы – үшбұрыштар); гексаэдрден шыққан қарапайым пішін – тригонтетрагексаэдр (24 жағы – тең үшбұрыштар); ерекше қарапайым пішіндері – ромбододекаэдр (12 жағы – ромб), пентагондодекаэдр (12 жағы – бес бұрыштар), дидодекаэдр (24 жағы – трапеция) (…11 суретке сәйкес).

1 2 3 4 5

6 7 8 9 10

11 12 13 14 15
1) тетраэдр, 2) тригонтритетраэдр, 3) тетрагонтритетраэдр, 4) пентагонтритетраэдр, 5) гексатертраэдр, 6) октаэдр, 7) тригонтриоктаэдр, 8) тетрагонтриоктаэдр, 9) пентагонтриоктаэдр, 10) гексаоктаэдр, 11) гексаэдр (куб), 12) тригонтетрагексаэдр, 13) ромбододекаэдр, 14) пентагондодекаэдр, 15) дидодекаэдр.
11 сурет – Жоғарғы категорияның, кубтық сингониясының қарапайым пішіндері
Фигураның қарапайым пішіндері ашық және жабық болуы мүмкін.
Қарапайым пішіннің жақтары өзара қиылысып, араларындағы кеңістікті түгел қауыстырған түрін жабық пішін деп атайды. Мысалы: куб қарапайым пішінге жатады, өйткені оның алты жағының бәрі бірдей шаршы және олары қауысып тұр. Жабық қарапайым пішіндерге кіретіндер: дипирамидалар, скаленоэдрлар, трапецоэдрлар, ромбоэдрлар, одан басқа тағы кубтық сингониясының қарапайым пішіндері.
Қарапайым пішінің жақтарының қиылыспай, араларындағы кеңістікті түгел қауыстырмайтын болса, оны ашық пішін деп атайды, олар өздігінен кездеспейді, тек комбинацияда. Мысалы, призма + пинакоид, пирамида + моноэдр. Ашық қарапайым пішіндерге кіретіндер: моноэдр, пинакоид, диэдр, призмалар және пирамидалар.
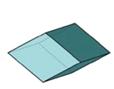
Қарапайым пішіннің бірнеше түрлері қауысқан пішіндерді комбинация деп атайды. Комбинацияда жабық пішіндерінің бірнеше біріккен түрлерінде кездеседі (…12 суретке сәйкес).
1  2
2 
1) призма және дипирамида комбинациясы, 2) текшемен ромбододекаэдрдің комбинациясы
12 сурет – Кристалдардың комбинациялары
Кристалдардың сингониялары, категориялары, симметрияларының түрлері, қарапайым пішіндерінің саңы және түрлері туралы мәліметтер кристалдық көп жақтылар туралы түсініктерді толығынан бермейді. Кристалдарды сипаттағанда олардың жақтарының кеңістікте бір-біріне қалай орналасқаны туралы білу қажет. Оны көрсету үшін кристаллографиялық символдар қолданады, олар кристалдың әр жағының координаттық өске салыстырмалы қалай орналасқанын бірқалыпты көрсетеді. Координаттық өстер көпшілігінде симметрия өстерімен және симметрия жазықтарымен сәйкес болады, немесе оларға перпендикуляр орналасады. Кейбір маңызды жағдайларды бөліп көрсетейік:
1. Бірлік жақтың символы әрқашан (111), оның координаттық өстерде тең әлде тең емес кесінділер қиюына байланысты емес.
2. Координаттық өстін біреуіне параллельді жақтың символында, сол өске сәйкес индекс ноль болады. (011) – 1-ші координаттық өске параллельді, (010) – 2-ші өсті қияды, (100) –жақ 1-ші координаттық өсті қияды және басқа екеуіне параллельді болады. Текшенің жалпы символы (100); октаэдрдің (111); тетраэдрдің (111); ромбододекаэдрдің (110).
Кристаллографиялық өстерді және бірлік жақтарды алғанда, немесе кристалды тұрғызып қойып зерттегенде, олардың симметрия өстері және симметрия жазықтардағы нормальдар, кристаллографиялық өстерге сәйкес деп саналады. Ортаңғы сингонияның кристалдарын ылғида тұрғызып қойғанда, оларды жоғарғы дәрежелі симметрия өсі тік орналасуы керек. Кубтық сингонияның кристалдары үш бір-біріне перпендикуляр L4 немесе L2 өстерге ие, оларды кристаллографиялық өстер деп санайды.
Негізгі әдебиеттер: [2, с. 5-15], [3, с. 12-13, 20-21];
Қосымша әдебиеттер: [8, с. 39-53], [10, с. 24-37]
Бакылау сүрақтары:
1. Кристалдар неден және қалай өседі?
2. Симметрия түрлерінің саны қанша; сингония және категория дегеніміз не, төменгі, ортаңғы және жоғарғы сингонияларының қарапайым пішіндері қандай болады?
3. Ашық және жабық қарапайым пішіндер, комбинациялар қандай болады?
Не нашли, что искали? Воспользуйтесь поиском: