Отличие архитектуры NetBurst от P6.

1. Использование кэш-памяти первого уровня для хранения декодированных команд (кэш трасс, 12 КМОП). Это позволяет разворачивать циклы, ускоряет декодирование за счет выборки уже декодированных команд.
2. Использование TBTB и TTLB для определения адресов в кэш трасс.
3. Механизм ранней спекулятивной диспетчеризации, заключающийся в продвижении на исполнение МОПов, ожидающих операнды уже обрабатываемых МОПов.
4. Разделение МОПов на медленные и быстрые.
5. Работа АЛУ на удвоенной частоте.
6. Увеличение длины ROB до 126 входов.
7. Увеличение размеров регистров замещения.
8. Увеличение размеров других буферов (BTB до 4096 и т.д.)
9. Слияние микроопераций загрузки/выгрузки и обработки.

Недостатки: высокая латентность конструкций, работающих с флагом переноса, высокая латентность команд сдвига, большая длина конвейера, малый размер L1D, малое быстродействие L2.

Особенности микроархитектуры NetBurst

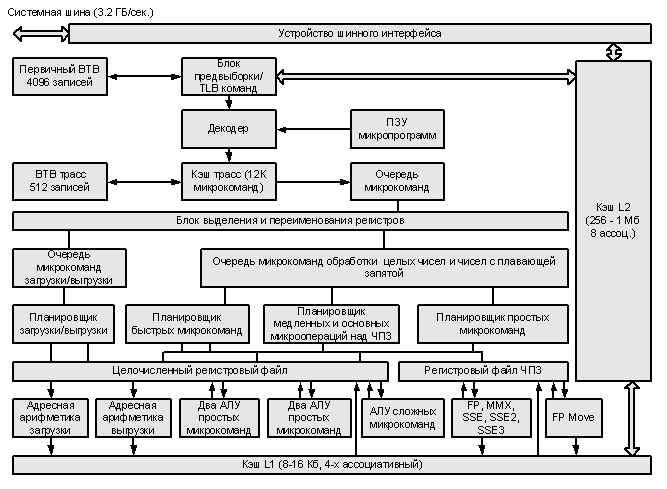
Планировщик в NetBurst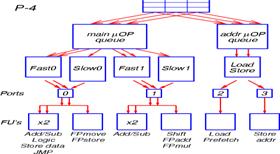

45. Аппаратные методы ускоренного умножения: умножители по схеме Уоллеса.

Умножение сводится к последовательному формированию частных произведений и их сложению. По способу формирования частных произведений: умножение со старших разрядов множителя со сдвигом влево, умножение с младших разрядов множителя со сдвигом вправо. По способу накопления частных произведений: матричные умножители, древовидные умножители.

Способы ускорения работы устройств умножения:

1. сокращение количества частных произведений;
2. обработка нескольких разрядов множителя за такт;
3. параллельное вычисление нескольких СЧП;
4. конвейеризация умножителей.

Принцип работы простейших косвенных умножителей:

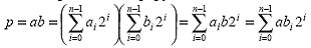
Для матричных и древовидных умножителей:

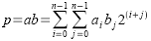
В наиболее общей формулировке дерево Уоллеса — это оператор с п входами и log2n выходами, в котором код на выходе равен числу единиц во входном коде. Вес битов на входе совпадает с весом младшего разряда выходного кода. Простейшим деревом Уоллеса является СМ. Используя такие сумматоры, а также полусумматоры, можно построить дерево Уоллеса для перемножения чисел любой разрядности, при этом количество сумматоров возрастает пропорционально величине log2n. В такой же пропорции растет время выполнения операции умножения.

Согласно алгоритму Уоллеса, строки матрицы частичных произведений группируются по три. Полные сумматоры используются для сжатия столбцов с тремя битами, а полусумматоры — столбцов с двумя битами. Строки, не попавшие

в набор из трех строк, учитываются в следующем каскаде редукции. Количество строк в матрице (ее высота) на j-й ступени определяется выражениями:

wо = n и w j + l =2[wj3] + (wj mod 3), пока wj >=2.

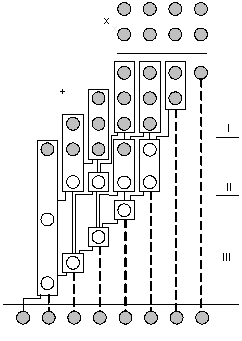
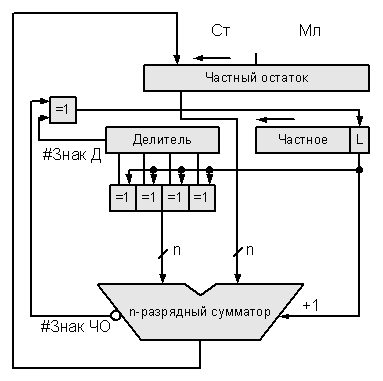
46. Деление с восстановлением и без восстановления остатка. Структура арифметико-логического устройства для целочисленного деления.

ЧО – частный остаток.

Деление с восстановлением остатка. Деление без восстановления остатка.

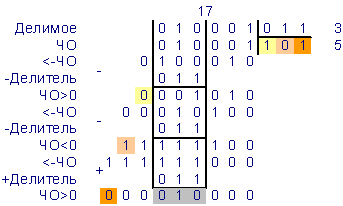
Алгоритм1:

1) ЧО = Делимое;

2) ЧО = ЧО*2;

3) ЧО = ЧО – Делитель * 2ⁿ;

4) Если ЧО<0 то

Ч<-0,

ЧО = ЧО + Делитель * 2ⁿ

иначе Ч<-1;

5) Если все цифры то конец

иначе пункт 2.

Алгоритм2:

1) ЧО = Делимое*2;

2) ЧО = ЧО – Делитель * 2ⁿ;

3) ЧО = ЧО*2;

4) Если ЧО<0 то

Ч<-0,

ЧО = ЧО + Делитель * 2ⁿ

иначе

Ч<-1;

ЧО = ЧО – Делитель * 2ⁿ

5) Если все цифры то конец

иначе пункт 3.

Схема АЛУ для целочисленного деления.

47. Организация операций сложения, умножения и деления над числами с плавающей запятой (ЧПЗ).

Подготовительный этап.

Разделение упакованного ЧПЗ на группы М,П,З (мантисса, порядок, знак).

Проверка на специальное числовое значение.

Выполнение операции.

Приведение порядков.

Определение знака результата.

Определение мантиссы результата.

Определение порядка результата.

Проверка на переполнение, потери значимости мантиссы, потери значимости порядка, неточности, деления на 0.

Заключительный этап.

Проверка на специальное числовое значение.

Нормализация результата.

Проверка на переполнение, потери значимости мантиссы, потери значимости порядка, неточности, деления на 0.

Упаковка полей З,П,М в ЧПЗ.

Алгоритм сложения и вычитания:

Подготовительный этап

Определение меньшего из двух порядков и проведение операции выравнивания порядков (сдвиг вправо на разность порядков).

Проверка на потерю значимости одного операнда (неточность).

Определение результирующего порядка как максимума.

Сложение мантисс и определение знака результата.

Проверка на переполнение мантиссы. Если до то сдвигаем мантиссу вправо и увеличиваем порядок на 1.

Проверка на переполнение порядка.

Заключительный этап.

Алгоритм умножения:

Подготовительный этап

Проверка (M1=0 или M2=0). Если да, то Р=0.

Определение порядка результата: Пр = П1+П2-С.

Проверка на переполнение порядка.

Определение мантиссы результата: Мр = М1*М2.

Определение знака результата.

Заключительный этап.

Алгоритм деления:

Подготовительный этап

Проверка (M1=0 или M2=0). Если деление на ноль, то +/-бесконечность или ошибка.

Определение порядка результата: Пр = П1-П2+С.

Проверка на переполнение порядка.

Определение мантиссы результата: Мр = М1*(1/М2).

Определение знака результата.

Заключительный этап.

Не нашли, что искали? Воспользуйтесь поиском: