Методические указания по выполнению практических и контрольной работ

Задачи изучения дисциплины - овладеть знаниями общих основ статистической науки: современными методологиями, методами и приемами сбора, обработки, обобщения и анализа статистической информации о социально-экономических явлениях и процессах, а также выработать навыки количественного исследования и анализа статистической информации, формирующейся на предприятии, в отрасли, в народном хозяйстве.

Методические указания по выполнению практических и контрольной работ

Чтобы облегчить самостоятельную работу при решении практических и контрольной работ по дисциплине, следует ориентироваться на учебный материал лекций в учебниках, представленных в рекомендательном библиографическом списке, и руководствоваться методическими указаниями по их выполнению, приведенными ниже.

При выполнении задачи 1 необходимо усвоить сущность статистической свод­ки и группировки, их виды, а также основные правила образования групп по количественным признакам.

Задачу следует начинать с определения группировочного (факторного) признака. Факторным является признак, оказывающий влияние на другие, связанные с ними признаками.

Признаки, изменяющиеся под влиянием факторного, называются результативными.

Затем определяют количество групп «n» по формуле Стерджесса при известной численности совокупности «N»

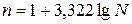(1)

Величина интервала определяется по формуле:

(2)

где x_max и x_min — соответственно максимальное и мини­мальное значения факторного признака;

n - число групп

Далее, при построении аналитической группировки по имеющимся данным нужно:

- сгруппировать имеющиеся данные по факторному признаку;

- по каждой группе исчислить средние значения результативного признака, вариация которого от группы к группе под влиянием группировочного признака будет указывать на наличие или отсутствие взаимосвязи между этими признаками.

По результатам группировки необходимо дать анализ и сделать выводы.

Для графического изображения зависимости в прямоугольной системе координат откладываются по оси х значения группировочного признака - фактора, а по оси у – средние значения зависимого изучаемого признака. При наличии интервалов значения зависимого признака наносят на ординатах, проходящих через середины интервалов.

В методических указаниях представлен пример решения подобной задачи (пример 1).

При выполнении задачи 2 необходимо правильно сделать выбор вида и формы средней. Это зависит от сущности осредняемого признака, его логичес­кой связи с другими признаками, от содержания и наличия исходного ма­териала и задач статистического исследования.

Если статистические данные представляют собой отдельные значения варьирующего признака (варианты) Х и соответствующие им частоты (число случаев повторения признака X) f, то для определения среднего признака X применяется средняя арифметическая взвешенная:

(3)

Если в условии даны варианты Х и объемы признаков W (произве­дения X на f), то для расчета среднего значения признака необходимо использовать среднюю гармоническую взвешенную:

, (4)

В практической деятельности средняя величина представляет собой обобщенную количественную характеристику и не позволяет принять решения в пользу какого-либо варианта (например, варианта вложения капитала). Для окончательного принятия решения необходимо измерить колеблемость показателей, т.е. определить меру изменчивости возможного результата.

Колеблемость возможного результата представляет собой степень отклонения ожидаемого значения от средней величины. Для этого на практике обычно применяют два близко связанных критерия: дисперсию и среднее квадратическое отклонение. Они служат мерами абсолютной колеблемости. Для анализа обычно используют коэффициент вариации, показывающий степень отклонения полученных значений. Коэффициент вариации – относительная величина. Поэтому на его размер не оказывают влияния абсолютные значения изучаемого признака. С помощью коэффициента вариации можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации может изменяться от 0 до 100 %. Чем больше коэффициент, тем сильнее колеблемость. В экономической статистике установлена следующая оценка различных значений коэффициента вариации: до 10 % - слабая колеблемость; до 10 – 15 % - умеренная колеблемость; свыше 25 % - высокая колеблемость. На практике принимается тот вариант, который имеет наименьшую колеблемость возможного результата.

Средний квадрат отклонений значений признака от средней арифметической (дисперсия) в вариационном ряду определяется по формуле:

или (5)

Корень квадратный из дисперсии представляет собой среднее квадратическое отклонение:

или (6)

Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак.

Отношение среднего квадратического отклонения к средней величине называется коэффициентом вариации и выражается обычно в процентах:

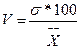(7)

Три последних вопроса задачи 2 относятся к теории выборочного наблюдения. Статистика использует различные схемы формирования выборочной совокупности: случайную, типическую, серийную. При этом возможны повторный и бесповторный способы отбора единиц в выборку. В зависимости от спо­соба отбора изменяются и формулы, по которым необходимо вы­числять численность выборки, ее среднюю и предельную ошибку (таблица 1).

где п — численность единиц выборочной совокупности;

N — число единиц генеральной совокупности;

n_C — число выборочных серий;

Nc — число серий генеральной совокупности;

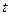— нормированное от­клонение (коэффициент доверия);

σ ² — дисперсия выборочной совокупности;

— серийная дисперсия;

— внутригрупповая (остаточная) дисперсия;

ω — частость (выборочная доля), т. е. доля единиц выборочной совокупности, обладающая данным признаком;

— остаточная дисперсия альтернатив­ного признака.

Нужно отличать долю отбора (для количест­венного признака)

n / N (8)

от выборочной доли

ω = m / n *100 (9)

где m – число единиц, обладающих изучаемым признаком.

Нормированное отклонение (t) функционально связано с вероят­ностью (p). Эти теоретические величины выступают в выборочном методе в качестве нормативов оценки выборочных характеристик. В таблице 2 представлены значения вероятности при различной величине коэффициента доверия.

Следует иметь в виду, что границы генеральной средней () опреде­ляются значением выборочной средней () и предельной ошибкой выборки для средней (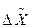). Они записываются формулой:

(10)

Чтобы определить границы генеральной доли (P), необходимо найти выборочную долю (ω) и предельную ошибку выборочной доли (). Генеральная доля равна:

(11)

Таблица1

Не нашли, что искали? Воспользуйтесь поиском: