Найти уравнение зависимости - это значит определить параметры уравнения: и .

Параметр a₁ называется коэффициентом регрессии и характеризует, в какой мере увеличивается у_х с ростом на единицу величины x.

При линейной зависимости сохраняется одинаковый прирост функции на единицу изменения аргумента.

Теоретическая линия у_х должна пересечь ломанную не менее, чем в двух точках.

Для нахождения параметров уравнения могут быть использованы несколько методов: наиболее часто применяется метод наименьших квадратов.

Суть этого метода состоит в том, что прямая должна быть приведена таким образом, чтобы сумма квадратов отклонений точек, лежащих на ломаной от теоретической линии, должна быть минимальной.

На основе этого метода составляется система уравнений, позволяющих определить параметры прямой.

(19)

где п – численность совокупности.

Параметры уравнения можно определить также по следующим формулам:

, (20)

(21)

Проверка: (22)

В практике экономического анализа применяются следующие нелинейные функции зависимости: гиперболическая, параболическая, степенная, полулогарифмическая. Криволинейные формы зависимости характерны тем, что с изменением аргумента изменяется и функция, и ее прирост.

Если результативный признак с увеличением факторного признака возрастает (или убывает) не бесконечно, а стремится к конечному пределу, то для анализа такого признака применяется уравнение гиперболы:

(23)

Рис. 2. Выравнивание по гиперболе

Для определения параметров уравнения гиперболы используется система нормальных уравнений:

(24)

Чтобы определить параметры уравнения гиперболы методом наименьших квадратов, необходимо привести его к линейному виду. Для этого произведем замену переменных , получим следующую систему нормальных уравнений:

(25)

Если с возрастанием факторного признака происходит ускоренное возрастание или убывание результативного признака, то корреляционная зависимость может быть выражена параболой второго порядка:

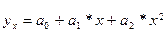(26)

Рис. 3. Выравнивание по параболе второго порядка

Для расчета параметров параболы второго порядка методом наименьших квадратов используется система нормальных уравнений:

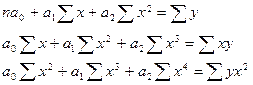(27)

Степенная функция вида

(28)

применяется в экономических исследованиях для характеристики слабо нелинейной

связи между результативными и факторными признаками. Параметр а₁ является

коэффициентом эластичности: с увеличением признака-фактора на 1 % результативный признак возрастает на а₁ процентов.

Для определения параметров степенной функции методом наименьших квадратов степенную функцию (28) необходимо привести к линейному виду путем логарифмирования. В результате получим уравнение вида

(29)

Заменим ; ;

Запишем уравнение (29) в новых обозначениях

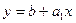(30)

Система нормальных уравнений для уравнения (30)

(31)

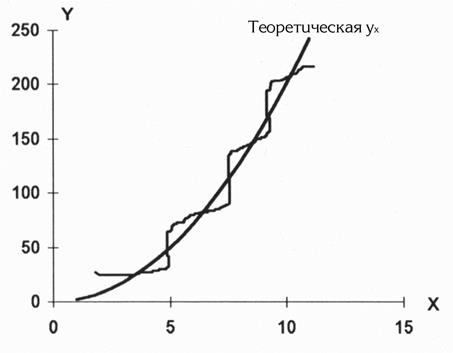
Рис.1.4. Выравнивание по степенной функции

Решая систему нормальных уравнений, определим параметры а₁ и b уравнения (31).

Переходя к первоначальным обозначениям , определяем параметр а₀.

Полулогарифмическая функция:

(32)

Рис. 5. Выравнивание по полулогарифмической функции

Для нахождения параметров полулогарифмической функции нужно решить

систему двух уравнений:

(33)

Все рассмотренные формы корреляционной связи относятся к корреляционной связи между двумя признаками: результативным и факторным. Такая зависимость называетсяпарной корреля­цией. Если на один результативный признак действует не один, а несколько факторов, то такая зависимость называетсямножественной корре­ляцией.

Случайная ошибка параметра а₁ (коэффициента регрессии) определяется по формуле:

(34)

где

(35)

Если фактическое превышение параметра своей случайной ошибки больше трех, то с большой вероятностью можно считать параметр не случайным, а значимым.

Коэффициент эластичности показывает, на сколько процентов возрастает у_х при увеличении х на один процент и рассчитывается по формуле:

(36)

Коэффициенты эластичности меняют свое значение с изменением величины x.

На рис. 1 изображены три линии: ломаная линия у – фактические данные; прямая наклонная линия у_х – теоретические значения при абстрагировании от влияния всех факторов, кроме фактора х; прямая горизонтальная линия – среднее значение, при исчислении которого исключено влияние на у всех без исключения факторов. Поэтому – это постоянная средняя, а у_х - переменная средняя, функционально изменяющаяся под влиянием изменения х. Как видно, переменная средняя отличается от постоянной, что говорит о силе влияния фактора х. Линия у_х не совпадает с линией у. Это свидетельствует о том, что связь между у и х неполная, нефункциональная. Следовательно, чтобы измерить тесноту связи, т.е. определить ее близость к функциональной связи, нужно исчислить дисперсию, измеряющую отклонения у от у_х и характеризующую остаточную вариацию, обусловленную прочими факторами. Разность между общей дисперсией, измеряющей отклонения у и и дисперсией, измеряющей отклонения у и у_х, представляет собой дисперсию, измеряющую вариацию, обусловленную фактором х. На сравнении этой разности с общей дисперсией построен индекс корреляции, или теоретическое корреляционное отношение:

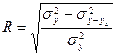; (37)

Или по формуле:

; (38)

где

(39)

Индекс корреляции характеризует зависимость y от x. Он приближенно равен эмпирическому корреляционному отношению и изменяется в пределах от 0 до +1.

При R равным 0 связь между вариацией признаков y и x отсутствует. Это происходит тогда, когда , иначе говоря, когда линия на рис.1. совпадет с линией , т.е. принимает горизонтальное положение и не реагирует на изменение величины x.

Когда индекс корреляции равен 1, то связь между y и x функциональная, полная. Это происходит тогда, когда , т.е. линия на чертеже сольется с линией у. Это означает, что изменение у целиком определяется изменением х.

Изменение происходит в пределах от 0 до . Чем меньше значение , тем ближе связь к функциональной.

Корреляционное отношение R пригодно для измерения тесноты связи при любой ее форме, но не показывает направление связи.

Более того, выравнивая значения у по разным функциям, мы можем по величине дисперсии, характеризующей остаточную вариацию () судить о том, какая функция в наилучшей степени выравнивает (аппроксимирует) эмпирическую линию связи.

Линейный коэффициент корреляции – частный случай общего коэффициента корреляции.

Он определяется по формуле:

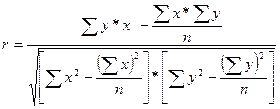(40)

Значение r изменяется от –1 до +1. Если r имеет знак минус, то связь обратная, если имеет знак плюс, то связь прямая. Близость к единице в том и другом случае характеризует близость к функциональной зависимости.

Для линейной формы связи значениякорреляционного от­ношения и линейного коэффициента корреляции совпадают. На этом факте основана проверка гипотезы о линейности зависимости.

Из формулы 41 можно определить а₁, не исчисляя уравнение связи:

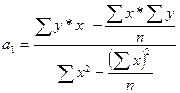(41)

В методуказаниях представлено решение аналогичной задачи (пример 4).

При выполнении задачи 5 необходимо вычислить аналитические показа­тели рядов динамики:

▪ цепные и базисные абсолютные приросты, темпы роста и темпы при­роста;

▪ абсолютное значение одного процента прироста (или уменьшения);

▪ среднегодовые темпы роста и темпы прироста;

▪ средний уровень ряда динамики;

▪ средний абсолютный прирост.

Приступая к решению задачи, следует усвоить, что для каждого отрезка времени в ряду динамики имеются уровень ряда Y и показатель времени t. В зависимости от качественной стороны уровня пока­зателя ряда динамики различают ряды абсолютных, относительных и сред­них величин; в зависимости от выбранных показателей времени ряды быва­ют интервальные и моментные. Интервальные ряды характеризуют развитие явления за определенные периоды (интервалы) времени (месяц, квартал, год), а моментные - на определенные моменты (даты) времени. Эти особенности необходимо учитывать при опреде­лении производных аналитических показателей рядов динамики, которые могут быть цепными и базисными.

Цепными называются показатели, которые получаются при сравнении каждого уровня ряда Y_i с предыдущим уровнем Y_i-1.

Базисными называются показатели, которые получают, если каждый уровень ряда сравнивается с одним и тем же исходным уровнем Yо, принятым за базу сравнения (например, первым уровнем ряда).

Абсолютные приросты (∆) исчисляют как разность уровней ряда и выражаются в единицах измерения показателей ряда.

Цепной абсолютный прирост равен:

(42)

Базисный абсолютный прирост определяется по формуле:

(43)

Относительные показатели динамики - темпы роста Тр и темпы при­роста Tпp характеризуют интенсивность процесса роста. При их расчётах важно обратить внимание на выбор базы для сравнения и помнить, что произведение цепных темпов роста всегда дает базисный темп роста.

Цепной темп роста определяется по формуле:

Тр = Y_i /Y_i-1 (44)

Базисный темп роста равен:

Тр = Y_{i /} Y₀ (45)

Его можно определить как произведение цепных темпов роста. Например, если взять данные за четыре года, то, перемно­жив три цепных темпа роста, получим соответствующий базисный темп:

Тр =Y₁ /Y₀*Y₂ /Y₁*Y₃ /Y₂ =T₁*T₂*T₃ =Y₃ /Y₀ (46)

Число перемноженных цепных темпов роста равно 3, что соответствует длине периода (три года). Аналогичный вы­вод можно сделать, если перемножить не три, а любое число m темпов роста.

Любой темп роста может быть выражен как в форме коэффициента (простого отношения уровней ряда), так и в процентах:

Тр (%) = Тр *100. (47)

Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился (или уменьшился) уровень ряда по сравнению с ба­зисным, принятым за 100 %. Поэтому он всегда на 100 % меньше соответс­твующего темпа роста:

Тпр (%) = (Тр - 1) * 100 = Тр (%) - 100 % (48)

Один и тот же процент прироста может означать различный абсолютный прирост. Поэтому нужно научиться определять абсолютное значение одного процента прироста или уменьшения (А). Значение последнего может быть определено делением цепного абсолютного прироста на цепной темп прироста, либо делением предыдущего уровня (или базового) на 100, т. е.:

(49)

(50)

При определении среднегодового темпа роста необходимо использо­вать среднюю геометрическую простую:

(51)

где Т ₁, Т₂, Т₃,...., Т_m, - цепные темпы роста;

m - число цепных темпов роста (их количество на единицу меньше, чем число уровней ряда динамики).

Можно пользоваться и другой формулой, которая имеет вид:

(52)

где n - число уровней ряда динамики в изучаемом периоде, не считая базисного;

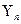и - конечный и начальный уровни ряда;

- базисный темп роста.

В некоторых учебниках встречается формула:

(53)

где уровень базисного периода обозначается Y₁, а n означает число всех уровней ряда динамики, включая базисный.

Среднегодовой темп прироста (среднегодовая относительная скорость роста) определяется по формуле:

(54)

При определении среднего уровня ряда динамики пользуются различными формулами. Их выбор зависит от вида ряда.

Для интервального ряда динамики с равноотстоящими уровнями во времени средний уровень ряда определяется по формуле средней арифметической простой:

, (55)

где ΣY – сумма уровней ряда динамики;

n – число уровней ряда.

Если интервальный ряд имеет неравноотстоящие уровни, то средний уровень ряда исчисляется по формуле средней арифметической взвешенной:

(56)

где t - число периодов времени, в течение которых уровень не изменился

Для моментного ряда динамики с неравноотстоящими уровнями, сред­ний уровень за весь период определяется по аналогичной формуле, при этом весами являются величины промежутков времени между датами:

(57)

где Y₁ - средний уровень за i – ый интервал времени между соседними датами;

t₁ - длина каждого интервала времени.

Для моментного ряда с уровнями, отстоящими друг от друга на рав­ные по продолжительности интервалы времени, средний уровень ряда можно вычислить по предыдущей формуле, либо по формуле средней хронологичес­кой, полученной из нее в результате некоторого преобразования.

(58)

где Y₁ – начальный уровень ряда;

Yn ^– последний уровень ряда;

n - число уровней ряда;

n-1 - число уровней ряда без одного, т.е. число периодов времени между датами

Среднегодовой абсолютный прирост (среднегодовую абсолютную скорость роста) можно найти как среднюю арифметическую годовых приростов, либо по формуле:

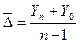(59)

где n - число уровней ряда динамики.

В методуказаниях представлено решение аналогичной задачи (пример 5).

При выполнении задачи 6 следует знать, что важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда). Это можно осуществить, применяя специальные методы анализа рядов динамики. Конкретное их использование зависит от характера исходной информации и предопределяется задачами анализа.

Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Главное в этом методе заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые и т. д.).

Для статистического изучения тренда применяется и сглаживание методом скользящей средней. В основу этого метода положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.

Для выявления основной тенденции развития методом скользящей средней прежде всего устанавливаются ее звенья. Звенья скользящей средней должны составляться из числа уровней, отвечающих длительности внутригодовых цикловизучаемого явления.

Для ряда динамики, отображающего развитие явления по кварталам, скользящие средние обычно составляются из четырехчленных звеньев. Их расчет состоит в определении средних величин из четырех уровней ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:

; (60)

и т.д (61)

Если при сглаживании рядов динамики звенья скользящей средней составляются из нечетного числа уровней, то необходимость в центрировании отпадает.

Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания, но получать обобщенную статистическую оценку тренда посредством этих методов невозможно. Решение задачи измерения тренда достигается методом аналитического выравнивания.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития рассчитывается как функция времени:

(62)

Подбор функции, с помощью которой производится определение теоретических (расчетных) уровней, осуществляется методом наименьших квадратов, т.е. сумма квадратов отклонений между расчетными (теоретическими) и эмпирическими уровнями должна быть минимальной:

(63)

Значение уравнения 63 состоит в том, что при изучении тренда оно принимается в качестве критерия оценки соответствия расчетных (теоретических) уровней с фактическими (эмпирическими) уровнями ряда динамики.

Одним из условий обоснованного применения метода аналитического выравнивания в анализе рядов динамики является знание типов развития социально-экономических явлений во времени.

Рассмотрим только некоторые из них.

Основная тенденция развития в рядах динамики со стабильными абсолютными приростами отображаются уравнением прямолинейной функции:

, (64)

где а₀ и а₁ – параметры уравнения;

t – обозначение времени.

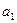(коэффициент регрессии) определяет направление развития.

Если 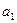> 0, то уровни ряда динамики равномерно возрастают, при 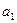< 0 – равномерно снижаются.

Основная тенденция развития в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка:

(65)

Значения параметров а₀ и а₁ идентичны параметрам, используемым в формуле 64. Параметр а₂ характеризует постоянное изменение интенсивного развития (в единицу времени). При > 0 происходит ускорение развития, при < 0 – замедление роста. Параметр 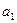может быть со знаком плюс или минус.

В рядах динамики, где показание цепного абсолютного прироста сокращается в конечных уровнях, основная тенденция развития выражается полулогарифмической функцией:

(66)

При аналитическом выравнивании в рядах динамики можно применить и другие математические функции:

степенную: (67)

функцию гиперболы: (68)

Для вычисления параметров указанных функций на основе метода наименьших квадратов составляются системы нормальных уравнений, которые приведены в методических указаниях к задаче 4 (формулы 19, 25, 27, 31, 33). Но х следует заменить на t.

Важно заметить, что для решения системы уравнений прямолинейной функции, обычно применяется способ определителей. Он позволяет более точно получить значения параметров за счет сведения к минимуму ошибки из-за округлений в расчетах.

Таким образом:

(69)

(70)

Для определения параметров математических функций при анализе тренда в рядах динамики кроме способа наименьших квадратов, может применяться и способ отсчета времени от условного начала. Он основан на обозначении в ряду динамики показаний времени таким образом, чтобы 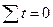и При этом в ряду динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевые значения и принимают его за условное начало отсчета времени с интервалом +1 всех последующих уровней и –1 всех предыдущих уровней. Например, при n = 5 обозначения времени будут –2, -1, 0, +1, +2. (рис.6)

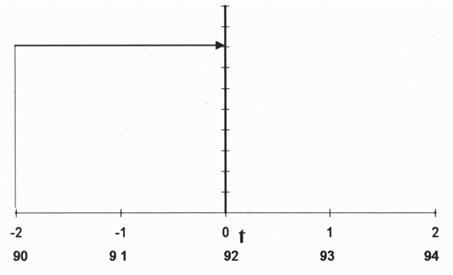
Рис. 6. Схема

При четном числе уровней, например n = 6, порядковые номера верхней половины ряда от середины обозначаются числами: -1, -3, -5, а нижней: +1, +3, +5. (рис. 7)

Рис. 7. Схема

При использовании способа условного обозначения времени, когда 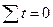и , параметры математической функции определяют по формулам:

а) для прямолинейной функции при

(71)

(72)

б) для функции параболы второго порядка при ,

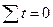(73)

Правильность расчетов параметров всегда проверяется по равенству:

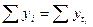(74)

По вычисленным параметрам производится синтезирование трендовой модели функции, т.е. полученные значения параметров подставляются в исходные функции. Затем, на основе модели определяются теоретические уровни тренда () для каждого года анализируемого ряда динамики.

Большое значение при определении прогнозов динамики каких-либо явлений имеют статистические методы экстраполяции. Под последней понимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее.

На практике прогнозные уровни определяют путем экстраполяции на основе среднего абсолютного прироста, аналитического выравнивания уровней ряда и цепных абсолютных приростов.

При использовании первого способа для определения прогнозного уровня необходимо прибавить средний абсолютный прирост к уровню, предшествующему планируемому.

При прогнозировании тренда изучаемого явления на основе аналитического выравнивания для его экстраполяции применяется адекватная трендовая модель, в которую подставляется значение t, равное определяемому периоду.

Для определения прогнозного уровня на основе выравнивания цепных абсолютных приростов необходимо использовать методику аналитического выравнивания с помощью различных функций, а также для экстраполяции тренда использовать адекватную трендовую модель.

В методических указаниях в примере 5 показано решение экстраполяции.

Задача 7 Классификация индексов, представленная в таблице 4, поможет изучению теории индексов и использованию их в практической работе.

Таблица 4

Не нашли, что искали? Воспользуйтесь поиском: