
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
От величины стоимости ОПФ
| Группы предприятий по размеру ОПФ (млн. р.) | Число предприятий | ОПФ (млн. р.) | Произведенная продукция (млн. р.) | Среднесписочное число работающих | Продукция на одного работающего (р.) | Произведенная продукция на один рубль ОПФ | |||
| Всего по группе | В среднем на одно предприятие | Всего по группе | В среднем на одно предприятие | ||||||
| 1,0 - 2,2 | 1,66 | 5,6 | 1,87 | 6829,3 | 1,120 | ||||
| 2,2 - 3,4 | 27,4 | 3,04 | 26,5 | 2,94 | 8412,7 | 0,967 | |||
| 3,4 - 4,6 | 19,4 | 3,88 | 23,0 | 4,60 | 11825,2 | 1,185 | |||
| 4,6 - 5,8 | 15,2 | 5,07 | 15,9 | 5,3 | 12278,0 | 1,046 | |||
| 5,8 и выше | 27,1 | 6,77 | 43,3 | 10,83 | 30492,9 | 1,597 | |||
| Итого | 94,1 | 3,92 | 114,8 | 4,78 | 13302,4 | 1,219 |
В таблице 9 видно, что по мере возрастания технической оснащенности предприятий растет объем продукции в среднем на одно предприятие (рис. 8), и ясно видна прямая зависимость показателей эффективности от величины стоимости основных фондов.
Эффективность работы промышленных предприятий зависит не только от размера ОПФ, но и от числа рабочих, использования оборудования и т. д. Отбирая разные факторные признаки и, уточняя систему показателей, можно дать разностороннюю характеристику взаимосвязи отдельных факторов.
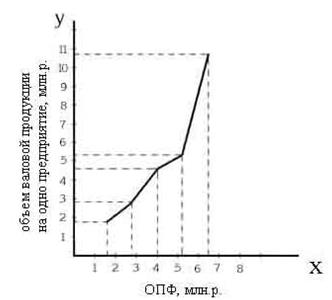
Рис. 8. Зависимость объема валовой продукции от размера ОПФ
Пример 2. На крупном хлебокомбинате в одном их цехов работают 500 рабочих. В порядке случайной бесповторной выборки обследовано 100 человек, которые по уровню выработки продукции распределяются следующим образом (таблица 10):
Таблица 10
| Дневная выработка, т. | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 |
| Численность рабочих |
На основании этих данных вычислить:
1. Среднюю дневную выработку одного рабочего.
2. Дисперсию и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0,997 возможные пределы среднего значения дневной выработки всех рабочих.
5. С вероятностью 0,954 возможные пределы доли рабочих с дневной выработкой 60 т и более.
6. Объем выборки, чтобы с вероятностью 0,954 предельная ошибка выборки при определении средней дневной выработки обследованных рабочих не превышала 2 т.
7. Объем выборки, чтобы с вероятностью 0,954 предельная ошибка при определении доли рабочих с дневной выработкой 60 т. и более не превышала 6 %.
Решение
Для расчетов построим вспомогательную таблицу 11:
Таблица 11
| Дневная выработка, т. | 
| 
| 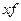
| 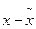
| 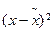
| 
| 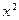
| 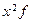
|
| 30 – 40 | -12 | |||||||
| 40 – 50 | -2 | |||||||
| 50 – 60 | ||||||||
| 60 – 70 | ||||||||
| Итого |
1. Средняя дневная выработка рабочего определяется по формуле 3:
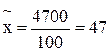 м.
м.
2. Дисперсия определяется по формуле 5:
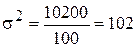
Среднеквадратическое отклонение определяется по формуле 6:
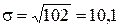
3. Коэффициент вариации определяется по формуле 7:
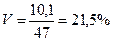
4. Средняя дневная выработка одного рабочего с вероятностью 0,997 определяется по следующей методике:
Средняя ошибка для средней (см. табл. 1)
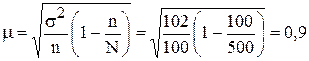
Предельная ошибка выборки для средней (см. табл.1), 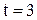 при Р = 0,997
при Р = 0,997

Таким образом, границы генеральной средней (формула 10):

Следовательно, верхняя граница генеральной средней: 47 + 2,7 = 49,7 м.
Нижняя граница: 47 – 2,7 = 44,3 м.
С вероятностью 0,997 можно утверждать, что средняя дневная выработка одного рабочего колеблется в пределах:
44,3 < 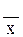 < 49,7
< 49,7
5. Доля рабочих (формула 9) с дневной выработкой 60 т и более с вероятностью 0,954 (t = 2)
Выборочная доля: 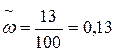
Средняя ошибка выборочной доли (см.табл.1):
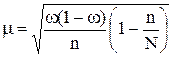
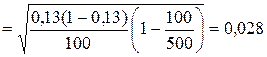
Предельная ошибка для доли (см. табл.1):
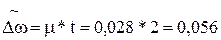
Таким образом, граница генеральной доли совокупности (формула 11)

- верхняя граница
0,13 + 0,056 = 0,186 (или 18,6 %)
- нижняя граница
0,13 – 0,056 = 0,074 (или 7,4 %)
С вероятностью 0,954 можно утверждать, что доля рабочих с дневной выработкой 60 т. и более колеблется от 7,4 % до 18,6 %.
6. Необходимая численность выборки при определении средней дневной выработки, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 2 т. (см. табл.1)
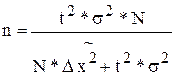 =
=  чел.
чел.
где 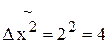
N = 500,
t = 2 при Р = 0,954

7. Объем выборки, чтобы с вероятностью 0,954 предельная ошибка при определении доли рабочих с дневной выработкой 60 т. и более не превышала 6 % (см. табл. 1).

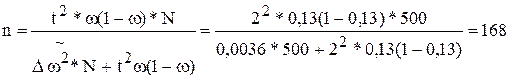 чел.
чел.
где 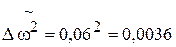
Пример 3
По данным аналитической группировки, полученной к задаче 1, измерить тесноту связи между результативным и факторным признаками, исчислив коэффициент детерминации и эмпирическое корреляционное отношение.
Решение
Составим вспомогательную таблицу 12
Таблица 12
| Группы предприятий по величине ОПФ, млн.р. | Число предприятий,

| Валовая продукция, млн.
р.
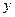
| Валовая продук-ция на одно пред-
приятие, млн.р.

| 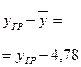
| 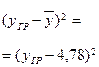
| 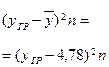
|
| 1—2,2 | 5,6 | 1,87 | -2,91 | 8,468 | 25,40 | |
| 2,2—3,4 | 26,5 | 2,95 | -1,83 | 3,349 | 30,14 | |
| 3,4—4,6 | 23,0 | 4,60 | -0,18 | 0,032 | 0,16 | |
| 4,6—5,8 | 15,9 | 5,30 | 0,52 | 0,270 | 0,81 | |
| 5,8 и выше | 43,3 | 10,95 | 6,17 | 38,069 | 152,28 | |
| Итого | 114,8 | 4,78 | 208,79 |
Средний выпуск продукции на одно предприятие в целом.
Общая средняя по формуле средней арифметической простой по формуле 55 будет равна:
 млн.р.
млн.р.
Дисперсия, характеризующая вариацию выпуска продукции за счет изменения основных фондов, т. е. межгрупповая дисперсия, по формуле 14:
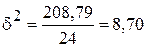
Общая дисперсия по индивидуальным данным (задача 1), используя формулу 17:
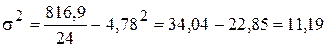
Для расчетов построим вспомогательную таблицу 13.
Таблица 13
| Номер предприятия | у | у2 | Номер предприятия | 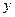
| у2 | Номер предприятия | у | У2 |
| 3,2 | 10,24 | 2,5 | 6,25 | 3,6 | 12,96 | |||
| 9,6 | 92,16 | 3,5 | 12,25 | 8,0 | 64,0 | |||
| 1,5 | 2,25 | 2,3 | 5,29 | 2,5 | 6,25 | |||
| 4,2 | 17,64 | 1,3 | 1,69 | 2,8 | 7,84 | |||
| 6,4 | 40,96 | 1,4 | 1,96 | 1,6 | 2,56 | |||
| 2,8 | 7,84 | 3,0 | 9,0 | 12,9 | 166,41 | |||
| 9,4 | 88,36 | 2,5 | 6,25 | 5,6 | 31,36 | |||
| 11,9 | 141,61 | 7,9 | 62,41 | 4,4 | 19,39 | |||
| Итого | 114,8 | 816,90 |
Коэффициент детерминации по формуле 12 равен:
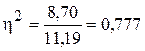
Корреляционное отношение по формуле 13 равно:
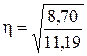 =
= 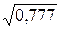 = 0,882
= 0,882
Вывод. Связь (табл.3) между размером ОФ и выпуском продукции высокая. Вариация выпуска продукции на 77,7% обусловлена вариацией стоимости ОФ.
Задача 4. По данным 24 предприятий (задача 1) построить корреляционную таблицу для исследования связи между размером ОПФ и производством валовой продукции. Найти уравнение регрессии. Изобразить эмпирические и теоретические данные на графике. Вычислить линейный коэффициент корреляции и корреляционное отношение. Сформулировать выводы.
Решение
Для всех последующих расчетов составим вспомогательную таблицу 14.
Таблица 14

| 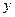
| 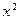
| 
| 
| 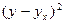
|
| 1,0 | 1,6 | 1,0 | 1,6 | -0,48 | 4,33 |
| 2,0 | 1,5 | 4,0 | 3,0 | 1,32 | 0,03 |
| 2,0 | 2,5 | 4,0 | 5,0 | 1,32 | 1,39 |
| 2,7 | 2,3 | 7,29 | 6,21 | 2,58 | 0,08 |
| 2,8 | 2,8 | 7,84 | 7,84 | 2,76 | 0,002 |
| 3,0 | 3,2 | 9,0 | 9,6 | 3,12 | 0,006 |
| 3,0 | 1,4 | 9,0 | 4,2 | 3,12 | 2,96 |
| 3,1 | 3,0 | 9,61 | 9,3 | 3,30 | 0,09 |
| 3,1 | 2,5 | 9,61 | 7,75 | 3,30 | 0,64 |
| 3,1 | 3,6 | 9,61 | 11,16 | 3,30 | 0,09 |
| 3,3 | 6,4 | 10,89 | 21,12 | 3,66 | 7,51 |
| Продолжение табл. 14 | |||||
| 3,3 | 1,3 | 10,89 | 4,29 | 3,66 | 5,57 |
| 3,5 | 7,9 | 12,25 | 27,65 | 4,02 | 15,05 |
| 3,5 | 2,5 | 12,25 | 8,75 | 4,02 | 2,31 |
| 3,9 | 4,2 | 15,21 | 16,38 | 4,74 | 0,29 |
| 4,0 | 2,8 | 16,0 | 11,2 | 4,92 | 4,62 |
| 4,5 | 5,6 | 20,25 | 25,2 | 5,82 | 0,05 |
| 4,7 | 3,5 | 22,09 | 16,45 | 6,18 | 7,18 |
| 4,9 | 4,4 | 24,01 | 21,56 | 6,56 | 4,66 |
| 5,6 | 8,0 | 31,36 | 44,8 | 7,8 | 0,04 |
| 6,5 | 9,4 | 42,25 | 61,1 | 9,42 | 0,0004 |
| 6,6 | 11,9 | 43,56 | 78,54 | 9,60 | 5,29 |
| 7,0 | 9,6 | 49,0 | 67,2 | 10,32 | 0,52 |
| 7,0 | 12,9 | 49,0 | 90,3 | 10,32 | 6,66 |
| 94,1 | 114,8 | 429,97 | 560,2 | 114,8 | 69,368 |
Уравнение регрессии определим по формуле 18, а его параметры по формуле 19.
Подставим значения и получим следующую систему уравнений:


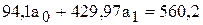
61 а 1 =110,1
а 1 = 1,8
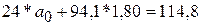
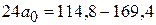
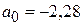
Уравнение линейной связи:
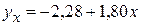
Таким образом, можно определить  для всех значений х (см. табл. 14).
для всех значений х (см. табл. 14).
Проверка значений параметров уравнения осуществляется по формуле 1.22 (см. табл. 14).
Индекс корреляции определяется по формуле 37.

Составляющая формулы 37 определяется по формуле 39:

Полученное значение индекса корреляции свидетельствует о тесной связи между размером ОФ и выпуском валовой продукции.
Случайная ошибка коэффициента регрессии (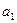 ) определяется по формуле 34:
) определяется по формуле 34:
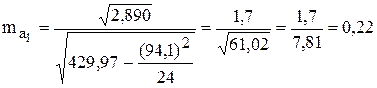
Коэффициент регрессии в примере равен 1,8. Он в 8,2 раза превышает случайную ошибку (1,8:0,22). Если фактическое превышение параметра своей случайной ошибки больше трех, то с большей вероятностью можно считать параметр не случайным, а значимым.
Коэффициент эластичности определяется по формуле 36.
В примере коэффициент эластичности на втором предприятии при х = 1 будет равняться:

Следовательно, на 1 % прироста стоимости ОФ на втором предприятии рост произведенной продукции составит 2,73 %.
Линейный коэффициент корреляции определяется по формуле 40. Его применение ограничено линейной формой связи.
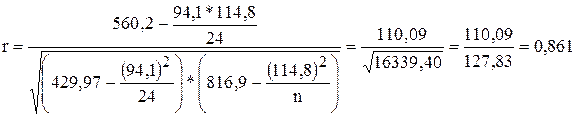
По формуле 41 можно определить коэффициент регрессии, не исчисляя уравнения связи:

По данным таблицы 14 построим теоретическую и эмпирическую линии регрессии производства валовой продукции (рис. 9). Эмпирическая линия свидетельствует о том, что не всегда с увеличением стоимости ОФ на предприятии возрастает объем валовой продукции.
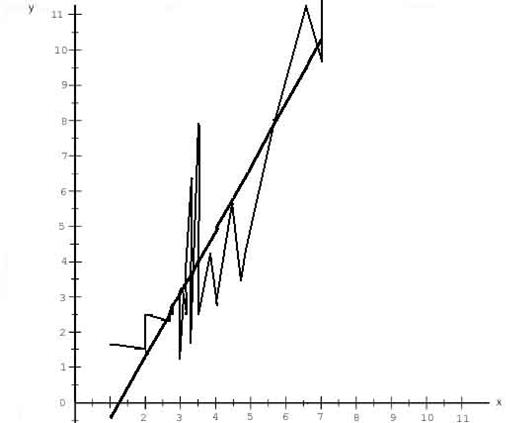
Рис. 9. Теоретическая и эмпирическая линии регрессии производства валовой продукции
Пример 5. На основе данных (табл. 15)
Таблица 15
| Годы | |||||||
| Товарооборот, млн.р. |
1. Определить все аналитические показатели ряда динамики. Показать взаимосвязь цепных и базисных темпов роста.
2. Произвести сглаживание ряда динамики с помощью скользящей средней и исчислить абсолютные и относительные приросты сглаженных уровней. Изобразить графически фактические уровни ряда и звенья скользящей средней.
3. Произвести аналитическое выравнивание ряда динамики по прямой. Изобразить графически фактические уровни и уровни, полученные при аналитическом выравнивании.
4. Найти методом экстраполяции ожидаемый уровень анализируемого показателя на 2013 год при условии сохранения основной тенденции:
а) на основе среднего абсолютного прироста;
б) на основе аналитического выравнивания уровне ряда;
в) на основе аналитического выравнивания цепных абсолютных приростов.
5. Определить относительное отклонение экстраполируемого уровня от фактического.
Решение
1. Аналитические показатели ряда динамики. Взаимосвязь цепных и базисных темпов роста.
Цепные и базисные абсолютные приросты, темпы роста, темпы прироста, абсолютное значение 1% прироста определяются по формулам 40-48. Результаты вычислений заносятся в таблицу 16.
Таблица 16
| Годы | Товарооборот, млн.т. | Цепные показатели | Базисные показатели | ||||||
| Абсолютный прирост, млн.р. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн.р. | Абсолютный прирост, млн.р. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн.р. | ||
| - | - | - | - | - | - | - | - | ||
| 110,0 | +10,0 | 0,20 | 110,0 | 10,0 | 0,20 | ||||
| 104,5 | +4,5 | 0,22 | 115,0 | 15,0 | 0,20 | ||||
| 108,7 | +8,7 | 0,23 | 125,0 | 25,0 | 0,20 | ||||
| 108,0 | +8,0 | 0,25 | 135,0 | 35,0 | 0,20 | ||||
| 103,7 | +3,7 | 0,27 | 140,0 | 40,0 | 0,20 | ||||
| 107,1 | +7,1 | 0,28 | 150,0 | 50,0 | 0,20 | ||||
| Итого |
Среднегодовой темп роста определяется по формуле 51. Число цепных темпов роста и число уровней ряда, не считая базисного, равно 6.
 или 107%
или 107%
 или 107%
или 107%
Данный расчет позволяет увидеть следующее: произведение цепных темпов роста дает базисный темп роста (формула 46).
Для нахождения корня логарифмируем выражение:

По таблице антилогарифмов определяем:
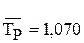 или
или 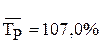
Среднегодовой темп прироста определяется по формуле 54 и равен:

Средний уровень ряда динамики определяется по формуле средней арифметической простой. Сумма уровней ряда равна 175 млн.р., а их число – 7.
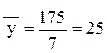 млн.р.
млн.р.
Среднегодовой абсолютный прирост определяется по формуле 59 и равен:
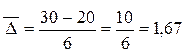 млн.р.
млн.р.
2. Сглаживание ряда динамики с помощью скользящей средней. Абсолютные и относительные приросты сглаженных уровней. Графическое изображение фактических уровней ряда и звеньев скользящей средней.
Для данного ряда динамики составим скользящие средние из трехчленных звеньев, т.е. примем шаг скольжения, равный трем.
Расчет скользящих средних представим в таблице 17 (см. методуказания к задаче 6).
Абсолютные и относительные приросты найдены по формулам 42, 48.
Таблица 17
| Год | Исходные уровни, 
| Скользящие средние, 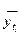
| Абсолютные приросты сглаженных уровней | Относительные приросты сглаженных уровней |
| --- | --- | --- | ||
| (20 + 12 + 23): 3 = 21,67 | --- | --- | ||
| (22 + 23 + 25): 3 = 23,33 | 1,66 | 7,7 | ||
| (23 + 25 + 27): 3 = 25,0 | 1,67 | 7,2 | ||
| (25 + 27 + 28): 3 = 26,67 | 1,67 | 6,7 | ||
| (27 + 28 + 30): 3 = 28,33 | 1,66 | 6,2 | ||
| --- | --- | --- |
Изобразим графически фактические уровни ряда и звенья скользящей средней (рис. 10)
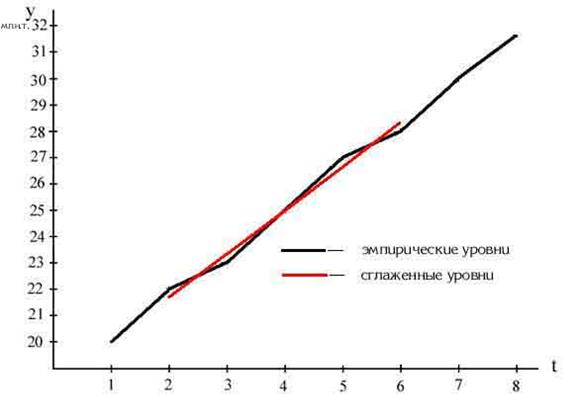
Рис. 10. Эмпирические и сглаженные уровни товарооборота
3. Аналитическое выравнивание ряда динамики по прямой. Графическое изображение фактических уровней ряда и уровней, полученных при аналитическом выравнивании.
Для определения параметров уравнения прямой

необходимо решить систему уравнений, которая принимает различный вид в зависимости от способа выражения временного фактора t.
Зададим t так, чтобы 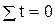 , т.е используем способ отсчета времени от условного начала. Тогда система двух нормальных уравнений
, т.е используем способ отсчета времени от условного начала. Тогда система двух нормальных уравнений

примет следующий вид:

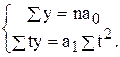
Для решения системы уравнений определяем 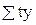 и
и  . Расчет представим в таблице 18 (см. графы 1-6).
. Расчет представим в таблице 18 (см. графы 1-6).
Подставим результаты расчетов и определим параметры уравнения:

 ,
, 
Таким образом, теперь становятся понятными формулы 71, 72 для определения параметров уравнения прямой.
Таблица 18
| Год | 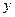
| 
| 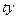
| 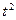
| 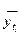
| 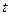
| 
| 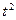
|
| -3 | -60 | 20,08 | ||||||
| -2 | -44 | 21,72 | ||||||
| -1 | 23,36 | |||||||
| 25,00 | ||||||||
| 26,64 | ||||||||
| 28,28 | ||||||||
| 29,92 | ||||||||
| Итого |
Получим уравнение  = 25 + 1,64 t.
= 25 + 1,64 t.
Подставляем в данное уравнение значения t и находим теоретические уровни ряда:
при t1 = -3 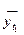 = 25 - 1,64 * 3 = 20,08;
= 25 - 1,64 * 3 = 20,08;
при t2 = -2 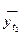 = 25 - 1,64 * 2 = 21,72 и т.д.
= 25 - 1,64 * 2 = 21,72 и т.д.
Полученные теоретические уровни расположены на одной прямой и характеризуют основную тенденцию изменения добычи угля за рассматриваемый период.
Для определения параметров уравнения методом наименьших квадратов, зададим t в виде натурального ряда: 1, 2, 3,..., п, Решая систему двух нормальных уравнений

определим значения Σt, Σt2 и Σty (см. гр. 7-9 табл.1.18).
Подставим:


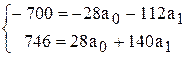
46 = 28 а1
а1 = 1,64
Находим а0:
175 =7 a0 + 28 * 1,64; 175 = 7 а0 + 45,92; 129,08 = 7 а0; а0 =18,44.
Для решения системы уравнений применяется способ определителей (формулы 1.69, 1.70):
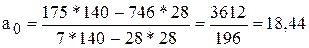
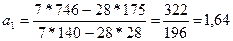
Имея параметры уравнения, получим уравнение прямой:
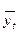 = 18,44 + 1,64 t.
= 18,44 + 1,64 t.
Подставляя в данное уравнение значения t, определяем  :
:
при t1 =1  = 18,44 + 1,64 * 1 =20,08;
= 18,44 + 1,64 * 1 =20,08;
при t2 =2 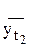 = 18,44 + 1,64 * 2 = 21,72 и т.д.
= 18,44 + 1,64 * 2 = 21,72 и т.д.
Таким образом, был получен тот же выровненный ряд уровней, что и в первом случае.
Изобразим графически фактические уровни ряда и теоретические (расчетные) уровни, полученные при аналитическом выравнивании (рис. 11)
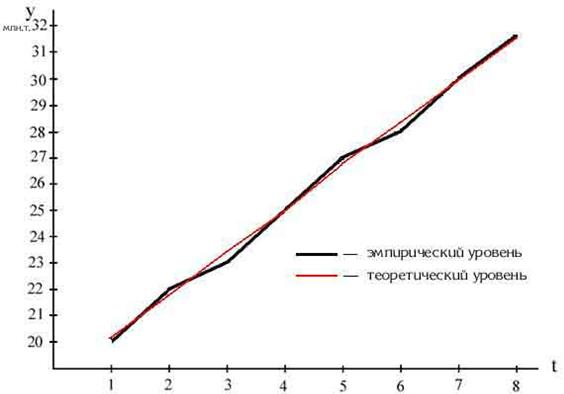
Рис.11. Эмпирический и теоретический уровни товарооборота
4. Ожидаемый уровень анализируемого показателя на 2013 год методом экстраполяции при условии сохранения основной тенденции:
а) на основе среднего абсолютного прироста
Прогнозное значение добычи угля на 2013 год определим, прибавив к уровню 2012 г. года значение среднего абсолютного прироста
30 + 1,67 = 31,67 млн.р.
Относительное отклонение планируемого уровня от уровня 2012 года:
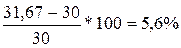
б) на основе аналитического выравнивания уровней ряда
Экстраполируя выявленную тенденцию в развитии, можно определить ожидаемый уровень на предстоящий период. Для этого подставим в полученную модель значение t, которое выходит за пределы эмпирического ряда. В нашем примере t = 4, применяя первый способ определения параметров уравнения. Тогда ожидаемый уровень составит:
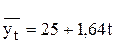
 =25+1,64 * 4 = 31,56 млн.р.
=25+1,64 * 4 = 31,56 млн.р.
И  , используя для определения параметров уравнения метод наименьших квадратов. В этом случае ожидаемый уровень равен:
, используя для определения параметров уравнения метод наименьших квадратов. В этом случае ожидаемый уровень равен:
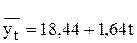
 млн.р.
млн.р.
Относительное отклонение планируемого уровня от уровня 2012 года:
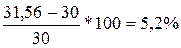
в) на основе аналитического выравнивания цепных абсолютных приростов
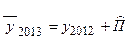
где 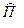 - средний прирост за период, экстраполированный путем аналитического выравнивания цепных приростов
- средний прирост за период, экстраполированный путем аналитического выравнивания цепных приростов
Так, цепные приросты выравниваем по прямой. Все расчеты для определения параметров уравнения методом определителей приведем в таблице 19.
Таблица 19
| Годы | П | 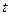
| 
| 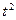
|
| Итого |

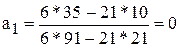

Для 2013 года t = 7, а 
Значит, ожидаемый уровень равен:
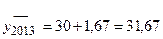 млн.т.
млн.т.
Относительное отклонение экстраполируемого уровня от фактического – 5,2 %.
Пример 6. По двум предприятиям имеются следующие данные (табл.20) о себестоимости и объеме производства однотипной продукции:
Таблица 20
| Предприятия | Произведено, млн.т | Себестоимость 1 т., р | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| А | 1,8 | 2,0 | ||
| Б | 2,2 | 3,0 |
Определить:
1. Индивидуальные и сводный (агрегатный) индексы себестоимости 1 т. продукции.
2. Сумму экономи за счет снижения 1 т. на каждом предприятии и в целом на обоих предприятиях.
3. Изменение затрат на производство на каждом предприятии и в целом на обоих предприятиях.
4. Изменение средней себестоимости 1 т. продукции (в рублях и в процентах), в том числе за счет изменения себестоимости на каждом предприятии и за счет структурных сдвигов в объеме производства.
5. Абсолютный прирост затрат на производство продукции за счет увеличения физического объема продукции, а также за счет снижения себестоимости 1 т.: на каждом предприятии; в целом на обоих предприятиях.
6. Сумму экономии за счет снижения средней себестоимости, в том числе за счет снижения себестоимости на отдельных предприятиях и за счет структурных сдвигов в объеме производства продукции.
Решение
1. Сводный индекс себестоимости исчисляется по формуле:
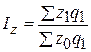
где  - затраты на производство всей продукции в отчетном периоде;
- затраты на производство всей продукции в отчетном периоде;
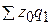 - затраты на производство всей продукции отчетного периода по себестоимости базисного периода.
- затраты на производство всей продукции отчетного периода по себестоимости базисного периода.
Тогда
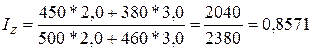 , или 85,7 %.
, или 85,7 %.
Следовательно, себестоимость продукции на двух предприятиях снизилась в среднем на 14,3%.
2. Сумма экономии, или дополнительных затрат, за счет изменения себестоимости определяется на основании индекса себестоимости:
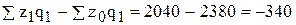 (млн.р.)
(млн.р.)
в том числе на первом предприятии: 900 – 1000 = - 100 (млн.р.).
3. Зная, что 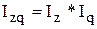 предварительно определяем индекс физического объема производства по формуле:
предварительно определяем индекс физического объема производства по формуле:

Тогда:
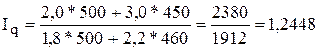 , или 124,5 %
, или 124,5 %
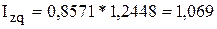 , или 106,7 %,
, или 106,7 %,
т. е. затраты на производство в целом на обоих предприятиях возросли на 6,7%.
4. Сводный индекс себестоимости переменного состава исчисляется по формуле
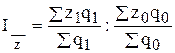
Тогда
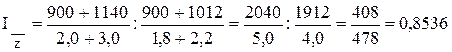 ,
,
или 85,4 %
Следовательно, средняя себестоимость 1 т. продукции снизилась на 70 р. (408 - 478), или на 14,6%.
Сводный индекс себестоимости постоянного состава исчисляется по формуле:

Тогда:
 , или 85,7 %
, или 85,7 %
Следовательно, средняя себестоимость 1 т. продукции снизилась на 68 р. (408 - 476), или на 14,3%, за счет снижения себестоимости продукции на отдельных предприятиях.
Сводный индекс структурных сдвигов исчисляется по формуле:
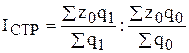
Тогда:
 или 99,6 %
или 99,6 %
Следовательно, средняя себестоимость 1 т. продукции снизилась на 2 р. (476 - 478), или на 0,4%, за счет структурных сдвигов в объеме производства.
5. Изменение затрат на производство продукции за счет отдельных факторов определяется следующим образом (по первому предприятию):
а) за счет увеличения физического объема производства продукции:
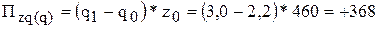 (млн.р.),
(млн.р.),
б) за счет изменения себестоимости 1 т. продукции:
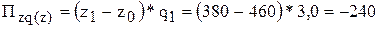 (млн.р.)
(млн.р.)
Затраты на производство продукции по первому предприятию в целом увеличились на 128 млн.р. (+368-240).
Аналогично определяется изменение затрат за счет отдельных факторов по второму предприятию.
Абсолютный прирост затрат на производство продукции на двух предприятиях в целом составит:
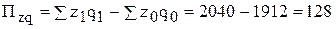 (млн.р.)
(млн.р.)
в том числе:
а) за счет увеличения физического объема производства:
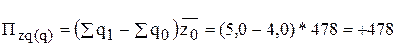 (млн.р.);
(млн.р.);
б) за счет изменения средней себестоимости 1 т. продукции:
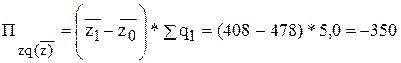 (млн.р.).
(млн.р.).
6. Экономия (350 млн. руб.) получена за счет двух факторов:
а) за счет структурных сдвигов b объеме производства:
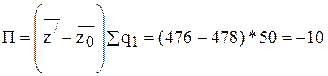 (млн.р.)
(млн.р.)
б) за счет снижения себестоимости 1 т. продукции на отдельных предприятиях:
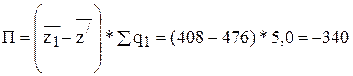 (млн.р.)
(млн.р.)
Пример 7. Имеются следующие данные по заводу (таблица 21):
Таблица 21
| Виды продукции | Затраты рабочего времени, чел-дни | Кол-во произведённой продукции, шт. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| А | ||||
| Б |
На основании приведенных данных определить:
1. Уровни производительности труда по каждому виду продукции отдельно в базисном и отчетном периодах.
2. Индивидуальные индексы производительности труда и трудоемкости.
3. Сводный индекс производительности труда: по форме агрегатного индекса; по форме среднего арифметического индекса.
4. Индивидуальные и сводные индексы общих затрат времени и физического объема продукции.
5. Экономию времени в результате роста производительности труда при производстве каждого вида продукции и в целом по всей продукции.
6. На сколько единиц продукции и процентов изменился объем производства за счет изменения затрат времени и производительности труда: по каждому виду продукции; в целом по всей продукции.
Решение
1. Индивидуальные индексы производительности труда могут быть исчислены по формулам:
а) 
б) 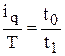
где 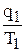 - уровень производительности труда в отчетном периоде (ω1);
- уровень производительности труда в отчетном периоде (ω1);
 - уровень производительности труда в базисном периоде (ω0);
- уровень производительности труда в базисном периоде (ω0);
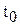 - затраты времени на единицу продукции (трудоемкость) в базисном периоде;
- затраты времени на единицу продукции (трудоемкость) в базисном периоде;
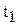 - затраты времени на единицу продукции (трудоемкость) в отчетном периоде.
- затраты времени на единицу продукции (трудоемкость) в отчетном периоде.
В данной задаче удобнее применить первую формулу (а).
Тогда:
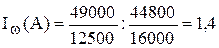

3. Сводный индекс производительности труда может быть исчислен:
а) по формуле агрегатного индекса:

где 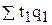 - общие затраты времени на всю продукцию в отчетном периоде;
- общие затраты времени на всю продукцию в отчетном периоде;
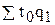 - общие затраты времени на всю продукцию отчетного периода при трудоемкости базисного периода.
- общие затраты времени на всю продукцию отчетного периода при трудоемкости базисного периода.
Тогда:
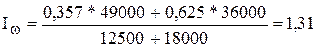
б) по формуле среднего арифметического индекса:
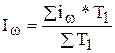

4. Сводный индекс общих затрат времени исчисляется по формуле:
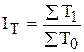
Тогда:
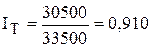
5. Сводный индекс физического объема продукции исчисляется по формуле:
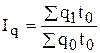
Тогда:

Этот индекс может быть исчислен и так:
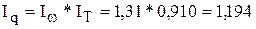
6. Общая экономия времени за счет роста производительности труда составила 9500 человеко-дней (30500 - 40000).
7. Прирост производства продукции за счет отдельных факторов составил:
а) за счет изменения затрат времени:
 шт.
шт.
б) за счет роста производительности труда:
 шт.
шт.
Не нашли, что искали? Воспользуйтесь поиском: