
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример карточки с заданиями по теме
«Иррациональные неравенства».
1. 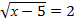 ;
;  .
.  ; 3.
; 3.  ;
;
4.  ; 5.
; 5. 
= 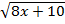 ;
;
6. 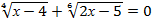 ; 7.
; 7.  ;
;
8.  = 0; 9.
= 0; 9. 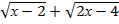 =10;
=10;
10. 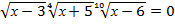 ; 11.
; 11. 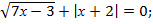
12. 
13.  ; 14.
; 14. 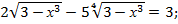
15. 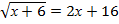 ; 16.
; 16.  ;
;
17. 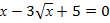 ; 18.
; 18.  ;
;
19. 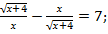 20.
20. 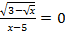 .
.
21.  22.
22. 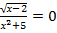
Ученик не должен решать данные на карточке неравенства, ему достаточно вспомнить и описать их решения по нескольким пунктам. Достаточно использовать этот метод с несколькими карточками, в течении 2-3-ёх занятий, после этого, более 60-70% детей вам скажут: «Я знаю, как это решать». Далее идёт умение выполнить действия и правильное вычисление, но это уже другая часть решения.
В любом случае есть исключения, от этого мы не застрахованы, бывает всё идёт по плану, а ученик приносит неожидаемую Вами оценку. Не расстраивайтесь, подумайте, какую ниточку подхода к ученику Вы упустили. В любом случае, Вы использовали правильный подход к решению, и об этом ученик вспомнит следующий раз.
И кто же здесь ШЕРЛОК?
Ещё более сложным становится вопрос - как заставить учить теоремы, аксиомы, и свойства в геометрии? И что надо сделать, чтоб после изучения теории, ученик начал ею пользоваться? Конечно, это не изучается за несколько уроков, многими учениками, для этого, даже года мало. Но если мы будем постоянно работать с этим вопросом, результат вас порадует.
Зачёт по геометрии с названием - «И кто же здесь ШЕРЛОК?», показывает, насколько хорошо Ваши учащиеся знают теорию, и могут ли использовать её на практике.
Для такого зачёта, очень подходит тема 8–го класса: «Четырехугольники», а так же несколько тем стереометрии 10-го класса, которые изучаются в первом полугодии. В этих темах, как раз много теоретической части, которую никто учить не хочет.
Обычный вопрос - что нам делать?
Превратить наших детей в Шерлоков…
Возьмём тему 8-го класса.
1. Выпишем на карточках все нужные нам теоремы, аксиомы, следствия из теорем и аксиом, то есть, всю теоретическую часть данной темы. Все карточки должны быть одного цвета, например жёлтые. На одной карточке, только одна теорема, или аксиома, или следствие.
2. На карточках, например, красного цвета, пишем тоже самое, пропуская некоторые слова, в правилах. Это сделано для того, чтоб ученики научились осмысливать запись правила и находить пропущенные слова или ошибки.
3. На карточках голубого цвета записываем задания, в которых среди данных правил, надо найти только одну правильную запись, или одну неправильную. (Такие задания можно найти в ЗНО, или в задачниках вспомогательной литературы.)
4. На карточках зелёного цвета, находятся рисунки, которые требуют доказательства с помощью знания или использования правил, на жёлтых карточках. Количество рисунков – 2 – 3, зависит от уровня сложности.
На этом подготовка к этой игре заканчивается.
Такие карточки Вы можете сделать сами.
А) На занятии.
Дать время ученикам повторить, или подучить жёлтые карточки.
Затем разложить колоду красных карточек, выбрать одну, и попробовать самостоятельно, без подсказки, найти ошибки. Если ученик самостоятельно ответить не может, он находит жёлтую карточку с нужным правилом, и объясняет ошибку. После, обе карточки, возвращаются в колоды, которые перемешиваются, далее действие повторяется. Это будет происходить до тех пор, пока ученик не даст самостоятельные ответы на вопросы 5-ти или 6-ти красных карточек.
Далее выбирается голубая карточка с голубой колоды. Если ученик, не отвечает самостоятельно на её вопрос, он также может найти ответы среди жёлтых карточек. Переход к зелёной колоде, будет выполнен после 5-ти или
6-ти голубых карт с правильными ответами.
Последнее задание с доказательством, также можно выполнить с помощью жёлтых карточек.
Конечно, здесь одним и даже двумя занятиями Вы не управитесь, но эти занятия помогут Вам сделать хоть какой-то шаг к получению желаемого результата.
Б) На зачёте.
Всё начинается с колоды красных карточек, затем голубые, затем зелёные.
Действия выполняются аналогично действиям на занятии, только для 10-ти красных карточек, разрешается помощь всего двух жёлтых.
Для 6-ти голубых карточек, в помощь даётся также две жёлтые.
И для одной зелёной, всего 2 жёлтые – те, которые попросит ученик.
Номинация «Шерлок», даётся тому, кто сдаст зачёт без единой подсказки жёлтой карточки. Это может быть маленький подарок, или сертификат вашего центра, или то, что придумаете Вы, а также позволит финансовое положение Вашего центра.
Постоянное прочтение правил теоретической части, хорошо влияет на зрительную память учеников, что очень помогает запомнить, изучить и разобраться в решении геометрических задач.
Разноцвет карточек выбирает тот, кто их делает.
| № 5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. |
| № 11. Диагонали параллелограмма пересекаются и делятся пополам |
| № 10. Диагонали параллелограмма пересекаются и точкой пересечения обязательно делятся |
| № 12. Диагонали четырехугольника пересекаются и точкой пересечения делятся пополам |
Здесь вы видите, что для одной жёлтой карточки может быть любое количество красных. И найти ошибки без помощи жёлтой карточки, довольно сложно.
| № 8 Являются ли правильными данные утверждения? А) Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник не ромб. Б) Если в параллелограмме диагонали не равны, то он не может быть прямоугольником. Ответы объяснить. |
№ 11. Докажите, что четырехугольник АВСD


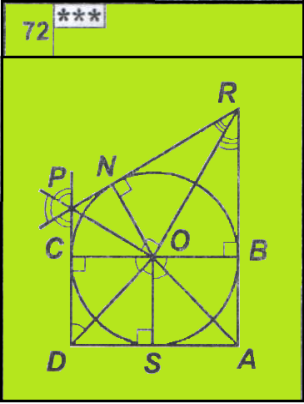 по данным рисунка - прямоугольник.
по данным рисунка - прямоугольник.
Если Вы в своих заданиях на зелёной карточке, дополнительно используете теоремы, или свойства другой темы, можете разрешить ученику пользоваться только страницей мини-справочника, например, с темой «Свойства круга». Если на рисунках для ответа достаточно использовать правила изучаемой темы, открывать справочники и учебники, не разрешается.
На ошибках учимся.
Часто мы говорим родителям, что их дети не внимательны,
из-за этого, допускаются ошибки и снижается оценка. Родители спокойно воспринимают наши доводы, и иногда говорят: «Ну, что ж тут сделаешь? Мы это знаем!» После этого разговора всё остаётся как прежде, без каких либо изменений. Обговорили и ЗАБЫЛИ!
А забывать то нельзя! Мы - особые учителя, мы – репетиторы! Как сказано раньше, это и психологи, и актёры, и писатели и художники и много ещё кто…
Конечно, это совсем не математика, но внимательность - очень нужна нашему предмету. Значит, что же нам снова делать?
1. Ввести курс упражнений на внимательность в начале занятий.
2. Можно сделать свой видео курс «Развитие внимательности» и проводить постоянные тренировки с учениками.
3. Часто проводить игру «На ошибках учимся».
Никто не заставляет Вас тратить на это половину занятия, но нулевой результат будет в том случае, если вы делать НИЧЕГО НЕ
БУДЕТЕ.
Уделив на это, хоть немного времени, думаю, не пожалеете.
Упражнения для своего курса, Вы можете найти на страницах интернета, а чтобы провести игру, надо приложить некоторые усилия.
Обратите внимания, какие ошибки делают ученики, изучая данную тему? Выбирая эти ошибки, записывайте их. Со временем у Вас накопится материал для игры. Создав большое количество карточек по разным темам, Вы избавите учеников от многих ошибок, если каких-то 5-7 минут времени ваши ученики затратят на их поиски в примерах.
Пример «ошибочной карты»
№ 5 Сколько ошибок в решении данного неравенства?
Тема: Как их исправить?
«Неравенства» 4 ≤ 5 – 8 х < 9
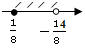 4 – 5 ≤ 5 – 5 – 8 х < 9 + 5
4 – 5 ≤ 5 – 5 – 8 х < 9 + 5
– 1 ≤ – 8 х < 14 /: (- 8)

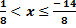 .
.
Ответ: 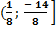
Объяснить все найденные ошибки.
Не нашли, что искали? Воспользуйтесь поиском: