Целые числа (теоретико-множественный подход)

Натуральное число, будучи характеристикой равномощных конечных множеств, может служить в то же время и характеристикой увеличения численности множества. Например, если мы имели конечное множество A (число элементов множества A обозначается п (А))и перешли к более широкому множеству B (число элементов множества В обозначается п (В)) (где п (А) < п (В)), то этот переход, характеризуется натуральным числом с = п (В) – п (А). Подобно этому и число 0 можно рассматривать не только как характеристику пустого множества (0 = п (Æ)), но и как характеристику отсутствия изменения численности множества, т.к. если п (А) = п (В); то п (В) – п (А) = 0.

Наряду с увеличением численности множества встречаются случаи ее уменьшения, тогда для выражения изменения численности множества недостаточно множества натуральных чисел. Для этого вводят отрицательные числа.

Определение. Целым отрицательным числом называется число, характеризующее уменьшение численности любого конечного множества А, на с элементов, т.е. замену этого множества А другим множеством В так, что: п (А) – п (В) = с, где п (А) > с.

Обозначаются целые отрицательные числа: –1, –2, –3,....

Таким образом, целое число можно определить как инвариант класса равномощных изменений численности конечных множеств. Причем изменения численности будут различаться по:

а) направлению (увеличение, уменьшение) мощности,

б) величине мощности.

Определение. Суммой двух данных целых чисел а и в называется целое число с, выражающее такое изменение численности множества, которое равносильно двум последовательно произведенным ее изменениям, выраженным числами а и в.

Причем разность определяется так:

с = а – в Û а = в + с.

Определение. Произведением целых чисел а и в называется целое число, обозначаемое как ав и определяемое формулами:

а) а · 0 = 0;

б) а · 1 = а;

в) если в > 1, то а · в = ;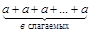

г) если в < 0, то а · в = – а · | в |.

Замечание. Здесь | в | – это модуль числа в.

Частное определяется так:

с = а: в Û а = в · с, причём в ≠ 0.

Не нашли, что искали? Воспользуйтесь поиском: