Преобразование обыкновенных дробей в десятичные

Выясним, при каком условии обыкновенная дробь может быть записана в виде десятичной дроби. Среди эквивалентных дробей выберем ту, числитель и знаменатель которой взаимно просты, такая дробь называется несократимой.

Например: – несократимые дроби.

Теорема. Обыкновенная несократимая дробь тогда и только тогда может быть записана в виде конечной десятичной дроби, когда каноническое разложение знаменателя имеет вид 2^a · 5^b.

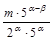Доказательство. Достаточность. Пусть n = 2 ^a · 5 ^b и пусть a ³ b. Тогда, умножая числитель и знаменатель данной дроби на 5 ^a-b, получим = = = = , т.е. обыкновенная дробь может быть записана в виде десятичной дроби с a десятичными знаками.

Необходимость. Пусть несократимая дробь может быть записана в виде , т.е. = .

Докажем, что знаменатель n не имеет простых множителей, отличных от 2 и 5.

По условию = , т.е. 10^a × m = e × n, но из этого следует 10^a× m n, а так как по условию теоремы дробь несократимая, следует, что 10^a n. Но в разложение 10^a на простые множители входят лишь 2 и 5, а потому и в разложение п будут входить только эти множители, т.е. n не может иметь простых множителей отличных от 2 и 5.

Из доказанной теоремы вытекает, что если знаменатель обыкновенной несократимой дроби делится хотя бы на одно простое число, отличное от 2 и 5, то эта дробь не представима в виде конечной десятичной дроби. Например, дробь не представима в виде конечной десятичной.

Не нашли, что искали? Воспользуйтесь поиском: