
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Несоизмеримые отрезки
Из предыдущего параграфа ясно, что два отрезка могут быть соизмеримыми или несоизмеримыми.
Определение 1. Два отрезка а и в называют соизмеримыми, если существует третий отрезок е, который укладывается в каждом из двух отрезков целое число раз, при этом отрезок е называется общей мерой этих двух отрезков.
Например, если имеем  то отрезки а и в соизмеримы.
то отрезки а и в соизмеримы.
Определение 2. Два отрезка а и в называют несоизмеримыми, если не существует третий отрезок е, который укладывается в каждом из двух данных отрезков целое число раз.
Докажем, что существует хотя бы одна пара несоизмеримых отрезков.
Еще в Древней Греции было замечено, что существуют отрезки, несоизмеримые с единичным отрезком е, т.е. отрезки длину которых нельзя выразить, пользуясь лишь рациональными числами. Так, один из учеников Пифагора в установленном Пифагором соотношении, что квадрат длины гипотенузы с прямоугольного треугольника равен сумме квадратов длин катетов, рассмотрел случай, когда длины катетов равны между собой и равны 1. Получив с 2 = 1 2 + 12, он поставил перед собой задачу найти с. Очевидно, что 1 < с < 2. Найти с путем подбора не удалось. Тогда были проведены для нахождения с такие общие рассуждения:
1) Допустим с =  , произвольная несократимая дробь.
, произвольная несократимая дробь.
2) Мы имеем ( )2 = 2Þ m 2 = 2 n 2 (*).
)2 = 2Þ m 2 = 2 n 2 (*).
3) Из (*) следует m 2  2, т.е. m – чётное, тогда обозначим m = 2 m 1. Подставим 2 m 1 в (*), получим (2 m 1)2 = 2 n 2 или 4 m 12 = 2 n 2 Þ 2 m 12 = n 2 Þ n 2
2, т.е. m – чётное, тогда обозначим m = 2 m 1. Подставим 2 m 1 в (*), получим (2 m 1)2 = 2 n 2 или 4 m 12 = 2 n 2 Þ 2 m 12 = n 2 Þ n 2  2.
2.
4) Из n 2  2 следует, что n – чётное, тогда обозначим n = 2 n 1.
2 следует, что n – чётное, тогда обозначим n = 2 n 1.
5) Таким образом  =
=  , дробь оказалась сократимой, но по условию она несократимая.
, дробь оказалась сократимой, но по условию она несократимая.
6) В рассуждениях получилось противоречие первоначальному предположению об её несократимости. Значит, допущение, что существует отрезок с, длина которою выражается дробным числом  ложно.
ложно.
Итак, длина отрезка с не выражается ни целым, ни дробным числом. Следовательно, существует хотя бы одна пара отрезков (сторона квадрата и его диагональ), длина одного из которых выражена числом 1, а длина другого не может быть при этом выражена ни натуральным, ни дробным числом, т.е. существуют несоизмеримые отрезки.
Для того, чтобы можно было выразить числом результат измерения любого отрезка лишь положительных рациональных чисел недостаточно, т.е. нужно расширить множество Q+, пополнив его новыми числами.
31. Отношение порядка на множестве
положительных действительных чисел
Отметим еще раз, что множество положительных действительных чисел является расширением множества положительных рациональных чисел. Рассмотрим теперь вопрос о сравнении положительных действительных чисел. Ранее мы установили, что соответствие между действительными положительными числами и бесконечными десятичными дробями не имеющими девять в периоде, взаимнооднозначное: каждому положительному действительному числу соответствует вполне определенная десятичная бесконечная дробь 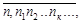 и, наоборот, каждая такая десятичная дробь является представлением вполне определенного действительного положительного числа.
и, наоборот, каждая такая десятичная дробь является представлением вполне определенного действительного положительного числа.
Рассмотрим два положительных действительных числа:
x =  и у =
и у =  .
.
Положительные действительные числа х и у считаются равными, если равны их целые части и соответствующие десятичные знаки,
т.е. х = у Û а = в, аi = вi (i = 1, 2, 3,...).
Если же целые части дробей различны или одна из дробей имеет десятичный знак, не совпадающий с соответствующим десятичным знаком другой дроби, то эти два положительных действительных числа считаются неравными.
Число х меньше числа у, если а < в или если найдется такое к,
что а = в, а 1 = в 1,..., ак -1= в к-1, но ак < вк.
Отношение «меньше» в множестве R+ антисимметрично, транзитивно и устанавливает в множестве R+ строгий линейный порядок.
В множестве R+ как и в множестве Q+ нет ни наименьшего, ни наибольшего числа. Кроме того, между любыми двумя числами из R+ лежит бесконечно много действительных чисел.
Очень важным свойством отношения порядка в множестве R+, которое отсутствует в Q+, является свойство непрерывности. Чтобы его сформулировать введем следующие понятия. Будем говорить, что числовое множество Х Ì R+ расположено слева от числового множества Y Ì R+, если для любых х Î Х и у Î Y выполняется неравенство х < у. Например, множество точек числового отрезка [2; 6] расположено слева от множества точек числового отрезка [8; 13]. Число 7 обладает тем свойством, что первое множество расположено слева от него, а второе справа. Говорят, что число 7 разделяет числовые отрезки [2; 6] и [8; 13].
Вообще, число с разделяет числовые множества Х и Y, если для любых х Î X, у Î Y имеем x £ c £ у.
Свойство непрерывности множества R+ формулируется так:
Если числовое множество Х расположено слева от числового множества Y, то найдется хотя бы одно число, разделяющее эти множества.
32. Сложение и умножение положительных действительных
чисел
Определим теперь сложение и умножение в R+ так, чтобы в частном случае, когда слагаемые являются положительными рациональными числами, эта операция совпадала с уже введенной нами операцией сложения положительных рациональных чисел.
Пусть даны положительные действительные числа:
x =  и
и
у =  .
.
В § 1 этой главы было показано, что при любом к имеем неравенства
xк £ x < x¢к и yк £ y < y¢к.
Число равное х + у должно быть заключено между числами (xк + yк) и (x¢к + y¢к), т.е. xк + yк £ x+ у < x¢к + y¢к при любом натуральном к.
Определение. Суммой двух положительных действительных чисел х и у называют такое число с, которое при любом натуральном k удовлетворяет неравенствам xк + yк £ с < x¢к + y¢к, т.е. с – число, разделяющее множества { xк + yк } и { x¢к + y¢к }.
Можно доказать, что такое число существует и является единственным. Мы ограничимся только иллюстрацией того, как данное определение суммы позволяет находить ее приближенное значение.
Пусть x = 3,247001..., у = 0,257702....
xк + yк= 3,504703, x¢к + y¢к = 3,504705, и мы можем написать пять верных знаков после запятой для определяемой суммы х + у =
= 3,50470....
Можно доказать, что операция сложения в множестве R+ коммутативна, ассоциативна и монотонна. Кроме того, ни для каких х и у из R+ не выполняется равенство х = х + у.
Определение. Произведением двух положительных действительных чисел х и у называют такое положительное действительное число р, которое при любом натуральном к удовлетворяет неравенствам xк × yк £ р < x¢к × y¢к, т.е. р – число, разделяющее множества { xк × yк } и
{ x¢к × y¢к }.
Операция умножения в R+ коммутативна, ассоциативна и дистрибутивна относительно сложения.
Операции вычитания и деления определяются как операции, обратные операциям сложения и умножения в R+ .
33. Вычитание и деление положительных
действительных чисел
Определение. Разностью двух положительных действительных чисел а и в (а > в) называют такое число с, которое в сумме с в дает а. Другими словами, разность с определяется как корень уравнения
в + с = а. Это уравнение в R+ имеет единственный корень при а > в. Обозначают разность а – в.
Покажем, например, как могут быть найдены приближенные рациональные значения разности  –
– 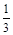 . Заменив в этом выражении число
. Заменив в этом выражении число  его любым десятичным приближением по недостатку, а число
его любым десятичным приближением по недостатку, а число 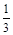 его любым десятичным приближением по избытку, мы получим, очевидно, приближенное рациональное значение разности
его любым десятичным приближением по избытку, мы получим, очевидно, приближенное рациональное значение разности  –
– 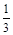 по недостатку, и наоборот, если в выражении
по недостатку, и наоборот, если в выражении  –
– 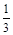 число
число  заменить его любым десятичным приближением по избытку, а число
заменить его любым десятичным приближением по избытку, а число 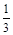 его любым десятичным приближением по недостатку, то полученная разность будет, очевидно, представлять собой приближенное значение
его любым десятичным приближением по недостатку, то полученная разность будет, очевидно, представлять собой приближенное значение  –
– 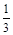 по избытку.
по избытку.
1,41421 £  < 1,41422; 0,33333 £
< 1,41422; 0,33333 £ 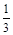 < 0,33334.
< 0,33334.
1,41421 – 0,33334 £  –
– 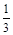 < 1,41422 – 0,33333,
< 1,41422 – 0,33333,
т.е. 1,08087 £  –
– 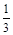 < 1,08089; значит,
< 1,08089; значит,  –
– 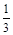 =1,0808....
=1,0808....
Определение. Частным от деления положительного действительного числа а на положительное действительное число в называют такое число с, которое при умножении на в дает число а.
Другими словами, частное с определяется как корень уравнения в × с = а. В R + это уравнение имеет единственный корень. Обозначают частное а: в.
Покажем, например, как могут быть найдены приближенные значения частного а: в, если а = 1,532..., в = 2,037...
Если в выражении а: в число а заменить его любым десятичным приближением по недостатку, а число в – его любым десятичным приближением по избытку, то полученное частное будет, очевидно, представлять собой приближенное значение а: в по недостатку. Наоборот, если в выражении а: в число а заменить любым его десятичным приближением по избытку, а число в – любым его десятичным приближением по недостатку, то полученное частное будет служить, очевидно, приближенным значением а: в по избытку.
В частности: 1,532: 2,038 £ а: в < 1,533: 2,037
0,7516 £ а: в < 0,7526 а: в = 0,75....
Не нашли, что искали? Воспользуйтесь поиском: