Отрицательные рациональные числа. Арифметические действия в множестве рациональных чисел.

Определение. Отрицательным рациональным числом – , где а и п – произвольные натуральные числа, называется число, характеризующее уменьшение любого множества «n -ных» долей элементов на а этих долей, т.е. замену множества, содержащего с «n -ных» долей, множеством, содержащим (с – а) таких долей.

После введения рациональных чисел обыкновенные дроби получают новое название – рациональные положительные числа и новое обозначение , + , . При п = 1 рациональные числа и представляют собой не что иное как целые числа +а и – а, а потому множество всех рациональных чисел, получаемое объединением всех рациональных положительных чисел, рациональных отрицательных чисел и числа 0, содержит в себе множество натуральных чисел N.

В записи будем считать теперь, что а Î Z, n Î N.

Итак, рациональное число, есть инвариант класса равномощных изменений численности конечных множеств, составленных из одинаковых долей элементов.

Определение. = , если дроби , одного знака и их модули равны, т.е. = .

Определение. Говорят, что

1) если и – положительные рациональные числа и ак > nв; или

2) если и – отрицательные рациональные числа и < ; или

3) если – положительное рациональное число, – отрицательное или равное 0 рациональное число.

Дальше определяются арифметические действия в множестве рациональных чисел.

Определение суммы в множестве рациональных чисел:

.

Определение произведения в множестве рациональных чисел:

.

Определение разности в множестве рациональных чисел:

.

Определение частного в множестве рациональных чисел:

, здесь а₂ ≠ 0.

24. Отношения «равно» и «больше» в множестве
положительных рациональных чисел. Основные свойства
множества положительных рациональных чисел

Эквивалентные (равные) дроби являются различными записями одного и того же положительного рационального числа. Например, эквивалентные дроби , , , …, , … 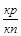– это различные записи одного и того же положительного рационального числа. Заметим, что = 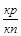Û p × (кn) = n × (кp).

Следовательно, два положительных рациональных числа

а ₁ = и а ₂ = равны тогда и только тогда, когда равны натуральные числа pt и sn.

Отношение равенства дробей обладает следующими свойствами:

1⁰. (" а, в Î N) [ = ] – рефлексивностью,

2⁰. (" а, в, с, d Î N) [ = Þ = ] – симметричностью,

3⁰. (" а, в, с, d, m, n Î N) [ = Ù = Þ = ] – транзитивностью.

Перейдем к рассмотрению отношения «больше» (>) в множестве положительных рациональных чисел.

Пусть а ₁ = , а ₂ = , где p, n, s, t Î N, тогда а ₁ > а ₂ Û pt > ns. Докажем это. Пусть , покажем, что тогда pt > ns. Дроби и приведём к общему знаменателю: и , так как > Û > (каждую дробь заменим равной ей), то pt > ns так как дроби теперь с одинаковыми знаменателями.

Обратно. Пусть теперь pt > ns, докажем, что > .

Разделим обе части данного неравенства на nt (оно ведь по свойству неравенств не нарушится). Получим > Û > .

Теперь мы можем сказать, какое из двух неравных положительных рациональных чисел больше другого, т.е. на множестве Q ₊ введено отношение «больше», которое обладает следующими свойствами:

1°. линейность: (" а ₁, а ₂ Î Q ₊) имеет место только одно из трёх соотношений: а ₁ = а ₂, либо а ₁ > а ₂, либо а ₁ < а ₂;

2°. транзитивность (" а ₁, а ₂, а ₃ Î Q ₊) [ a ₁ > a ₂ Ù a ₂ > a ₃ Þ a ₁ > a ₃];

3°. антисимметричность: ( а ₁, а ₂ Î Q ₊), для которых одновременно выполняются a ₁ > a ₂ и а ₁ < а ₂.

Значит, введённое отношение является отношением линейного порядка и, следовательно, множество Q ₊ линейно упорядочено.

Отношение порядка в Q ₊ обладает еще двумя свойствами:

1) в множестве Q ₊ нет ни наименьшего, ни наибольшего числа;

2) множество Q ₊ «плотно в себе».

Докажем 1). В самом деле, пусть а – какое-нибудь число из множества Q ₊. Представим его в виде дроби , p, n Î N. Но тогда дробь – запись числа, меньшего, чем а. Пусть теперь в какое-нибудь число из множества Q ₊, представим его в виде дроби , здесь
s, t Î N. Но тогда дробь – запись числа, большего, чем в.

Докажем свойство 2) в виде следующей теоремы.

Теорема 1. Между двумя любыми положительными рациональными числами а ₁ и а ₂, (а ₁ < а ₂) существует положительное рациональное число а ₃, такое, что а ₁ < а ₃ < а ₂.

Доказательство. По условию теоремы а ₁ < а ₂. Между этими числами существует по крайней мере одно положительное рациональное число, большее, чем а ₁, но меньшее, чем а ₂ и равное , т.к. операции сложения и деления не выводят нас из множества Q ₊. Далее между положительными рациональными числами а ₁и существует по крайней мере одно положительное рациональное число, равное и так далее. Т.е. между любыми двумя числами из множества Q ₊ расположено бесконечное множество положительных рациональных чисел, т.к. описанный выше процесс может быть продолжен неограниченно.

Отметим еще одно свойство множества Q ₊. Покажем, что множество Q ₊ счетно.

Теорема 2. Множество Q ₊ счетно.

Доказательство. Представим каждое рациональное число в виде дроби. Назовем высотой рационального числа сумму его числителя и знаменателя. Расположим все рациональные числа в порядке возрастания высоты, а числа одной и той же высоты – в порядке возрастания числителя. Покажем биективное отображение множества Q ₊ в множество N. Нумерацию чисел из Q ₊ проведем по следующей схеме:

Q +:										…
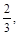
N:	1,	2,	3,	4,	5,	6,	7,	8,	9,	…

Но мы знаем, что каждое положительное рациональное число бесконечно многими способами может быть представлено в виде дроби , m, п Î N, например, =…. Поэтому, если мы перенумеруем все дроби, как указано на схеме, то тем более окажутся перенумерованными все числа Q ₊. При этом каждому натуральному числу будет поставлено в соответствие одно и только одно рациональное число. А это говорит о том, что множество Q ₊является счетным.

Таким образом, множество Q ₊ является линейно упорядоченным, плотным в себе и счетным.

Не нашли, что искали? Воспользуйтесь поиском: