
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Бесконечные периодические десятичные дроби
Известно, что если знаменатель п несократимой дроби  в своем каноническом разложении имеет простой множитель не равный 2 и 5, то эта дробь не представима в виде конечной десятичной дроби. Если мы попытаемся в этом случае записать исходную несократимую дробь в виде десятичной, производя деление числителя на знаменатель, то процесс деления закончиться не может, т.к. в случае его завершения через конечное число шагов, мы получили бы в частном конечную десятичную дробь, что противоречит ранее доказанной теореме. Так что в этом случае десятичная запись положительного рационального числа а =
в своем каноническом разложении имеет простой множитель не равный 2 и 5, то эта дробь не представима в виде конечной десятичной дроби. Если мы попытаемся в этом случае записать исходную несократимую дробь в виде десятичной, производя деление числителя на знаменатель, то процесс деления закончиться не может, т.к. в случае его завершения через конечное число шагов, мы получили бы в частном конечную десятичную дробь, что противоречит ранее доказанной теореме. Так что в этом случае десятичная запись положительного рационального числа а =  представляется бесконечной дробью.
представляется бесконечной дробью.
Например, дробь 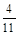 = 0,3636.... Легко заметить, что остатки при делении 4 на 11 периодически повторяются, следовательно, и десятичные знаки будут периодически повторяться, т.е. получается бесконечная периодическая десятичная дробь, которую можно записать так 0,(36).
= 0,3636.... Легко заметить, что остатки при делении 4 на 11 периодически повторяются, следовательно, и десятичные знаки будут периодически повторяться, т.е. получается бесконечная периодическая десятичная дробь, которую можно записать так 0,(36).
Периодически повторяющиеся цифры 3 и 6 образуют период. Может оказаться, что между запятой и началом первого периода стоит несколько цифр. Эти цифры образуют предпериод. Например,
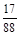 = 0,1931818... Процесс деления 17 на 88 бесконечен. Цифры 1, 9, 3 образуют предпериод; 1, 8 – период. Рассмотренные нами примеры отражают закономерность, т.е. любое положительное рациональное число представимо либо конечной, либо бесконечной периодической десятичной дробью.
= 0,1931818... Процесс деления 17 на 88 бесконечен. Цифры 1, 9, 3 образуют предпериод; 1, 8 – период. Рассмотренные нами примеры отражают закономерность, т.е. любое положительное рациональное число представимо либо конечной, либо бесконечной периодической десятичной дробью.
Теорема 1. Пусть обыкновенная дробь 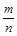 несократима и в каноническом разложении знаменателя n есть простой множитель отличный от 2 и 5. Тогда обыкновенная дробь
несократима и в каноническом разложении знаменателя n есть простой множитель отличный от 2 и 5. Тогда обыкновенная дробь 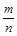 представима бесконечной периодической десятичной дробью.
представима бесконечной периодической десятичной дробью.
Доказательство. Мы уже знаем, что процесс деления натурального числа m на натуральное число n будет бесконечным. Покажем, что он будет периодическим. В самом деле, при делении m на n будут получаться остатки, меньшие n, т.е. числа вида 1, 2,..., (n – 1), откуда видно, что количество различных остатков конечно и потому, начиная с некоторого шага какой-то остаток повторится, что повлечет за собой повторение десятичных знаков частного, и бесконечная десятичная дробь становится периодической.
Имеют место еще две теоремы.
Теорема 2. Если в разложение знаменателя несократимой дроби на простые множители не входят цифры 2 и 5, то при обращении этой дроби в бесконечную десятичную дробь получится чистая периодическая дробь, т.е. дробь, период которой начинается сразу же после запятой.
Теорема 3. Если же в разложение знаменателя входят множители 2 (или 5) или тот и другой, то бесконечная периодическая дробь будет смешанной, т.е. между запятой и началом периода будет несколько цифр (предпериод), а именно столько, каков больший из показателей степеней множителей 2 и 5.
Теоремы 2 и 3 предлагается доказать читателю самостоятельно.
28. Способы перехода от бесконечных периодических
десятичных дробей к дробям обыкновенным
Пусть дана периодическая дробь а = 0,(4), т.е. 0,4444....
Умножим а на 10, получим
10 а = 4,444…4…Þ 10 а = 4 + 0,444….
Т.е. 10 а = 4 + а, получили уравнение относительно а, решив его, получим: 9 а = 4 Þ а = 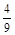 .
.
Замечаем, что 4 – одновременно и числитель полученной дроби и период дроби 0,(4).
Правило обращения в обыкновенную дробь чистой периодической дроби формулируется так: числитель дроби равен периоду, а знаменатель состоит из такого числа девяток, сколько цифр в периоде дроби.
Докажем теперь это правило для дроби, период которой состоит из п цифр. Пусть дана периодическая дробь
а =  . Умножим а на 10 n, получим:
. Умножим а на 10 n, получим:
10 n × а = 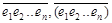 =
= 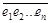 + 0,
+ 0,  ;
;
10 n × а = 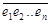 + a;
+ a;
(10 n – 1) а = 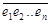 Þ a =
Þ a = 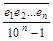 =
= 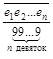 .
.
Итак, сформулированное ранее правило, доказано для любой чистой периодической дроби.
Пусть теперь дана дробь а = 0,605(43) – смешанная периодическая. Умножим а на 10 с таким показателем, сколько цифр в предпериоде, т.е. на 103, получим
103 × а = 605 + 0,(43) Þ 103 × а = 605 + 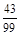 = 605 +
= 605 + 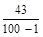 = =
= = 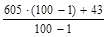 ,
,
т.е. 103× а = 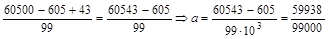 .
.
Правило обращения в обыкновенную дробь смешанной периодической дроби формулируется так: числитель дроби равен разности между числом, записанным цифрами, стоящими до начала второго периода, и числом, записанным цифрами стоящими до начала первого периода, знаменатель состоит из такого числа девяток, сколько цифр в периоде и такого числа нулей сколько цифр стоит до начала первого периода.
Докажем теперь это правило для дроби, предпериод которой состоит из п цифр, а период из к цифр. Пусть дана периодическая дробь
а = 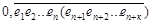 .
.
Обозначим в = 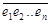 ; r =
; r = 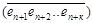 ,
,
с =  ; тогда с = в × 10 к + r.
; тогда с = в × 10 к + r.
Умножим а на 10 с таким показателем степени сколько цифр в предпериоде, т.е. на 10 n, получим:
а ×10 n = 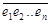 +
+ 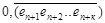 .
.
Учитывая введенные выше обозначения запишем:
а× 10 n = в +  .
.
Итак, сформулированное выше правило доказано для любой смешанной периодической дроби.
Всякая бесконечная периодическая десятичная дробь является формой записи некоторого рационального числа.
В целях однообразия иногда конечную десятичную дробь также считают бесконечной периодической десятичной дробью с периодом «нуль». Например, 0,27 = 0,27000...; 10,567 = 10,567000...; 3 = 3,000....
Теперь становится справедливым такое утверждение: всякое рациональное число можно (и притом единственным образом) выразить бесконечной десятичной периодической дробью и всякая бесконечная периодическая десятичная дробь выражает ровно одно рациональное число (периодические десятичные дроби с периодом 9 при этом не рассматриваются).
Не нашли, что искали? Воспользуйтесь поиском: