
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Понятие марковского случайного процесса.
Процесс работы СМО представляет собой случайный процесс. Под случайным (вероятностным или стохастическим) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями.
Процесс называется процессом с дискретными состояниями, если его возможные состояния  ,
,  ,…. можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком). Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны. Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем.
,…. можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком). Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны. Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем.
Математический анализ работы СМО существенно упрощается, если процесс этой работы — марковский. Случайный процесс называется марковским или случайным процессом без последствия, если для любого момента времени 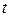 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t и не зависят от того, когда и как система пришла в это состояние.
вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t и не зависят от того, когда и как система пришла в это состояние.
При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой — так называемым графом состояний. Обычно состояния системы изображаются прямоугольниками (кружками), а возможные переходы из состояния в состояние — стрелками (ориентированными дугами), соединяющими состояния.
Пример 1. Построить граф состояний следующего случайного процесса: устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное случайное время.
Решение. Возможные состояния системы: 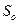 — оба узла исправны;
— оба узла исправны;  — первый узел ремонтируется, второй исправен;
— первый узел ремонтируется, второй исправен;  — второй узел ремонтируется, первый исправен;
— второй узел ремонтируется, первый исправен; 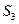 — оба узла ремонтируются. Граф системы приведен на рис. 1.
— оба узла ремонтируются. Граф системы приведен на рис. 1.
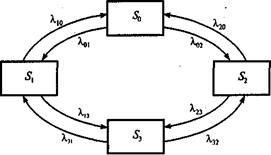
Рис. 1. Граф состояний устройства S
Стрелка, направленная, например, из 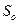 в
в  , означает переход системы в момент отказа первого узла, из
, означает переход системы в момент отказа первого узла, из  в
в 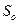 — переход в момент окончания ремонта этого узла.
— переход в момент окончания ремонта этого узла.
На графе отсутствуют стрелки из 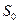 в
в 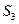 и из
и из 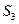 в
в 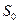 . Это объясняется тем, что выходы узлов из строя предполагаются независимыми друг от друга и вероятностью одновременного выхода из строя двух узлов (переход из
. Это объясняется тем, что выходы узлов из строя предполагаются независимыми друг от друга и вероятностью одновременного выхода из строя двух узлов (переход из 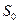 в
в 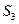 или одновременного окончания ремонтов двух узлов (переход из
или одновременного окончания ремонтов двух узлов (переход из 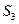 в
в 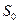 ) можно пренебречь.
) можно пренебречь.
Потоки событий.
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (например, поток вызовов на телефонной станции, поток отказов ЭВМ, поток покупателей и т.п.).
Поток характеризуется интенсивностью 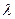 — частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.
— частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.
Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока есть величина постоянная: 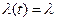 .
.
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени 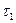 и
и 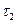 — число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
— число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени 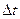 двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия.
Простейший поток в качестве предельного возникает в теории случайных процессов столь же естественно, как в теории вероятностей нормальное распределение получается в качестве предельного для суммы случайных величин: при наложении (суперпозиции) достаточно большого числа п независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивностям 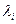 (
(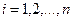 ) получается поток, близкий к простейшему с интенсивностью
) получается поток, близкий к простейшему с интенсивностью 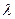 , равной сумме интенсивностей входящих потоков, т.е.
, равной сумме интенсивностей входящих потоков, т.е.
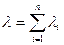 .
.
Не нашли, что искали? Воспользуйтесь поиском: