Уравнения Колмогорова. Предельные вероятности состояний.

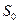Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем на примере случайного процесса из примера 10.1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями (); так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока "окончаний ремонтов" первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 6.6.1). Рассмат­риваемая система S имеет четыре возможных состояния: , , ,. .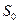

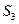Вероятностью i-го состояния называется вероятность того, что в момент t система будет находиться в состоянии . Очевид­но, что для любого момента сумма ероятностей всех состояний равна единице: . (8)

Рассмотрим систему в момент и, задав малый промежуток 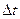, найдем вероятность того, что система в момент будет находиться в состоянии 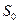. Это достигается разными способами.

1. Система в момент с вероятностью находилась в со­стоянии и за время 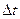не вышла из него. Вероятность того, что система будет находиться в состоянии 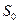в момент и не выйдет из него за время 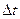, равна по теореме умножения вероятностей:

.

2. Система в момент с вероятностями или 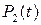находилась в состоянии или и за время 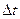перешла в состояние 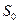. Система перейдет в состояние 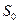с вероятностью, приближенно равной или . Вероятность того, что система будет перейдет в состоянии 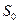по этому способу, равна или .

Применяя теорему сложения вероятностей, получим

= + + , откуда

= + + .

Переходя к пределу при , полу­чим в левой части уравнения производную : = + + .

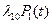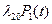Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы S, можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

= + + ,

= + + ,

= + + ,

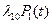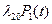= + + . (9)

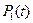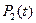+ + + = 1.

Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производ­ная вероятности i-го состояния. В правой части — сумма произве­дений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент t = 0. Так, например, систему уравнений (6.6.9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии 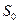, т.е. при на­чальных условиях: , , , .

Уравнения Колмогорова дают возможность найти все вероят­ности состояний как функции времени. Особый интерес представ­ляют вероятности системы в предельном стационарном режи­ме, т.е. при , которые называются предельными (или финаль­ными) вероятностями состояний.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии.

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описы­вающих стационарный режим. Для системы S с графом состоя­ний, изображенном на рис. 1), такая система уравнений имеет вид:

+ + = 0,

+ = 0,

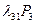+ = 0,

+ + = 0. (10)

Нормировочное условие:

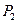+ + + = 1. (11)

Не нашли, что искали? Воспользуйтесь поиском: