
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Многоканальная система с отказами.
Рассмотрим классическую задачу Эрланга (Эрланг А.К. — датский инженер, математик конца XIX в. — начала XX в.). Имеется п каналов, на которые поступает поток заявок с интенсивностью 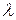 . Поток обслуживании имеет интенсивность
. Поток обслуживании имеет интенсивность 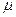 . Найти предельные вероятности состояний системы и показатели ее эффективности.
. Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): 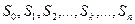 ,, где
,, где  — состояние системы, когда в ней находится k заявок, т.е. занято k каналов. Граф состояний СМО соответствует процессу гибели и размножения и показан на рис. 1.
— состояние системы, когда в ней находится k заявок, т.е. занято k каналов. Граф состояний СМО соответствует процессу гибели и размножения и показан на рис. 1.

Рис. 1. Граф состояний многоканальной СМО с отказами
Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью 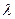 . Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии
. Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии  (два канала заняты), то она может перейти в состояние
(два канала заняты), то она может перейти в состояние  (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет
(один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет  . Аналогично суммарный поток обслуживании, переводящий СМО из состояния
. Аналогично суммарный поток обслуживании, переводящий СМО из состояния 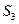 (три канала заняты) в
(три канала заняты) в  , будет иметь интенсивность
, будет иметь интенсивность 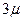 , т.е. может освободиться любой из трех каналов и т.д.
, т.е. может освободиться любой из трех каналов и т.д.
Для предельной вероятности состояния:  (1)
(1)
где члены разложения 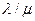 ,
, 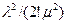 , …,
, …,  будут представлять собой коэффициенты при
будут представлять собой коэффициенты при 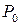 в выражениях для предельных вероятностей
в выражениях для предельных вероятностей  ,
, 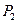 , …,
, …, 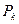 , …,
, …, 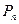 . Величина:
. Величина: 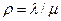 (2)
(2)
называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала. Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки. Теперь
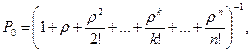 (3)
(3)
 ,
, 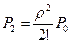 , …,
, …, 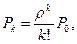 …,
…,  . (4)
. (4)
Формулы (3) и (4) для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового обслуживания. Вероятность отказа СМО есть предельная вероятность того, что все п каналов системы будут заняты, т.е.
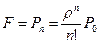 . (5)
. (5)
Относительная пропускная способность — вероятность того, что заявка будет обслужена: 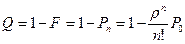 , (6)
, (6)
Абсолютная пропускная способность:  , (7)
, (7)
Среднее число занятых каналов  есть математическое ожидание числа занятых каналов:
есть математическое ожидание числа занятых каналов:
 ,
,
где 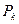 — предельные вероятности состояний, определяемых по формулам (3), (4).
— предельные вероятности состояний, определяемых по формулам (3), (4).
Однако среднее число занятых каналов можно найти проще, если учесть, что абсолютная пропускная способность системы А есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем 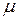 заявок (в единицу времени), то среднее число занятых каналов
заявок (в единицу времени), то среднее число занятых каналов
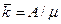 (8)
(8)
или, учитывая (6.6.29), (6.6.24):
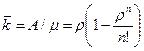 . (9)
. (9)
Пример 1. Имеется один канал, на который поступает поток заявок с интенсивностью 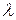 . Поток обслуживания имеет интенсивность
. Поток обслуживания имеет интенсивность 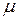 . Здесь и в дальнейшем предполагается, что все потоки событий, переводящие СМО из состояния в состояние, будут простейшими. К ним относится и поток обслуживания — поток заявок, обслуживаемых одним непрерывно занятым каналом. Среднее время обслуживания
. Здесь и в дальнейшем предполагается, что все потоки событий, переводящие СМО из состояния в состояние, будут простейшими. К ним относится и поток обслуживания — поток заявок, обслуживаемых одним непрерывно занятым каналом. Среднее время обслуживания 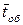 обратно по величине интенсивности
обратно по величине интенсивности 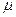 , т.е.
, т.е.  .
.
Определить оптимальное число печатных машин в типографии, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 95 заявок.
Решение. Интенсивность нагрузки канала по формуле (3)  = 0,1/0,2 = 0,5, т.е. за время средней продолжительности производственного цикла
= 0,1/0,2 = 0,5, т.е. за время средней продолжительности производственного цикла  = 5 ч поступает в среднем 0,5 заявок.
= 5 ч поступает в среднем 0,5 заявок.
Будем постепенно увеличивать число каналов (печатных машин)  = 2, 3, 4,... и определим по формулам (3), (6), (7) для получаемой
= 2, 3, 4,... и определим по формулам (3), (6), (7) для получаемой  -канальной СМО характеристики обслуживания. Например, при
-канальной СМО характеристики обслуживания. Например, при  = 2
= 2  = (l + 0,5 + 0,52/2!)-1 = 0,615;
= (l + 0,5 + 0,52/2!)-1 = 0,615;
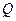 = 1- (0,52/2!)×0,615 = 0,923;
= 1- (0,52/2!)×0,615 = 0,923; 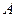 = 0,1×0,923 = 0,0923. Для n = 3
= 0,1×0,923 = 0,0923. Для n = 3  = (l + 0,5 + 0,53/3!)-1 = 0,657.
= (l + 0,5 + 0,53/3!)-1 = 0,657. 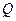 = 1- (0,53/3!)×0,657 = 0,986;
= 1- (0,53/3!)×0,657 = 0,986; 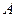 = 0,1×0,986 = 0,0986. Значение характеристик СМО сведем в табл. 1.
= 0,1×0,986 = 0,0986. Значение характеристик СМО сведем в табл. 1.
| Характеристика обслуживания | Число каналов (печатных машин) | ||
| Относительная пропускная способность Q | 0,66 | 0,923 | 0,986 |
| Абсолютная пропускная способность А | 0,066 | 0,0923 | 0,0986 |
По условию оптимальности Q ³ 0,95, следовательно, в типографии необходимо установить 3 телефонных номеров (в этом случае Q = 0,986 — см. табл. 1). При этом в час будут обслуживаться в среднем 0,0986 заявок (А = 0,0986), а среднее число занятых печатных машин (каналов) по формуле (8)  = 0,0986/0,2 = 0,493.
= 0,0986/0,2 = 0,493.
Не нашли, что искали? Воспользуйтесь поиском: