Необходимое условие дифференцируемости функции в точке

Функция, имеющая производную в точке , называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке промежутка , называется дифференцируемой на этом промежутке.

Теорема. Если функция 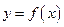дифференцируема в некоторой точке, то она непрерывна в этой точке.

Таким образом, непрерывность функции является необходимым условием дифференцируемости, но не является достаточным условием, т. к. производная - это предел отношения двух бесконечно малых, а этот предел может быть равен бесконечности или не существовать. Есл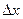и и именно таковы, то функция не будет дифференцируемой, будучи непрерывной.

Очевидно, что в соответствующей точке график функции либо не имеет определенной касательной (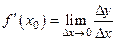 - не существует), либо угол наклона касательной к Оx равен (), т.е. касательная параллельна оси Oy.

Рис.1.2. Рис.1.3.

Не нашли, что искали? Воспользуйтесь поиском: