Прием логарифмического дифференцирования

Операция применения к функции сначала логарифмирования, а затем дифференцирования называется логарифмическим дифференцированием. Выражение называется логарифмической производной функции 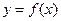. Таким образом, для нахождения производной получаем формулу логарифмического дифференцирования:

или

Прием логарифмического дифференцирования удобно применять:

· при нахождении производной функции, которая равна произведению большого числа множителей, сначала функцию логарифмируют, логарифм произведения множителей раскладывают в сумму логарифмов и дифференцируют. Найти производную суммы функций значительно легче, чем производную произведения нескольких функций;

· при нахождении производной степенно-показательной функции:

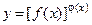, , поскольку основание степени и показатель зависят от 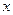, то применение формул для производной степенной или показательной функции невозможно. В этом случае:

, .

По формуле получаем

.

Например.

Найти производную функции . Имеем , , тогда .

Не нашли, что искали? Воспользуйтесь поиском: