Свойства функций, непрерывных на отрезке

Определение. Функция 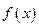называется непрерывной на отрезке , если она определена для любого и непрерывна в каждой точке этого отрезка (в точке a справа, в точке b слева)

1. Теорема Вейерштрасса. Всякая непрерывная на отрезке функция ограничена и достигает на нем своей верхней грани и своей нижней грани.

2. Теорема Больцано – Коши. Если функция 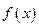непрерывна на и , , то для любого , заключенного между и , существует хотя бы одна точка , такая что .

Следствие. Функция 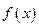, непрерывная на отрезке и принимающая на концах отрезка значения разных знаков, хотя бы в одной точке внутри отрезка обращается в , .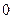

3. Теорема «О непрерывности обратной функции». Если функция определена, непрерывна и строго монотонна на отрезке , то обратная ей функция так же определена, непрерывна и строго монотонна на отрезке с концами в точках и .

Например, определена, непрерывна и строго возрастает на 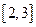. 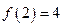, 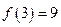. Тогда обратная функция определена, непрерывна и строго возрастает на отрезке .

Не нашли, что искали? Воспользуйтесь поиском: