Дифференцирование сложной функции. Пусть функция дифференцируема в точке и функция дифференцируема в точке ( ), тогда сложная функция дифференцируема в точке и её производная

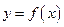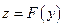Пусть функция дифференцируема в точке и функция дифференцируема в точке (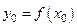), тогда сложная функция 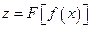дифференцируема в точке и её производная определяется формулой:

.

Таким образом, производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

Например.

Найти производную функции .

Здесь , , , Тогда, .

Не нашли, что искали? Воспользуйтесь поиском: