ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Дифференцирование сложной функции
Пусть 
- дифференцируемая функция переменных 
, которые сами являются дифференцируемыми функциями переменной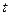 
: 
, 
, тогда полная производная сложной функции 
по аргументу 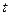выражается формулой:
В частности, если 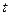совпадает с одной из переменных, например 
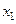, то полная производная функции 
по 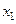равна:
Например.
В общем случае, если - дифференцируемая функция переменных , которые сами являются дифференцируемыми функциями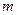 
переменных 
: 
, , частные производные сложной функции 
по аргументам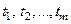 
выражаются формулами:
,
,
…………………………
.
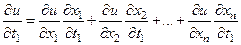Причём, переменные 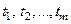называют независимыми аргументами функции 
, а переменные - зависимыми или промежуточными аргументами.
Например.
, 
.
, 
, 
, 
, 
, 
.
,
.
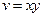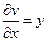Не нашли, что искали? Воспользуйтесь поиском: