Частные производные функции многих переменных

2.3.1. Определение частной производной и её геометрический смысл

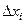Пусть дана функция . Зафиксируем все переменные, кроме одной , а переменной дадим приращение , тогда получим частное приращение функции по переменной :

- .

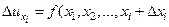
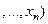Определение. Частной производной функции по переменной называется предел отношения частного приращения этой функции по переменной к приращению этой переменно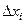й , при →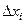

= = .

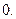
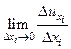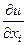Частную производную обозначают и другими символами: .

Вычислять частную производную функции многих переменных по одному аргументу следует по обычным правилам и формулам дифференцирования, в предположении, что все остальные аргументы - постоянные величины.

Например.

= +

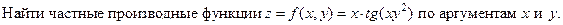
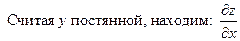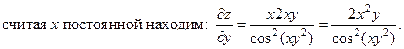
Частная производная функции двух переменных 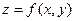, вычисленная по переменной 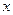в фиксированной 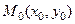выражает скорость изменения данной функции в направлении оси Ox или скорость изменения функции 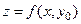одной переменной .

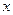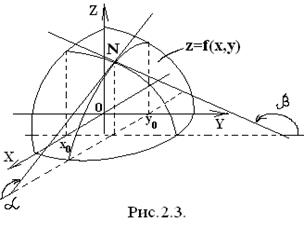Частные производные функции 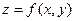в точке 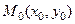имеют следующий геометрический смысл: 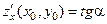и ,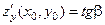

где α- угол между осью Ox и касательной проведенной в точке 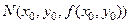к линии пересечения поверхности

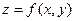и плоскости .

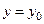β-угол между осью Oy и касательной в той же точке к линии пересечения поверхности 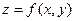и плоскости .

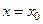Не нашли, что искали? Воспользуйтесь поиском: