ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Монотонность функции
Теорема “Признак монотонности функции”. Если функция 
дифференцируема на промежутке 
и её производная на этом промежутке положительна (отрицательна), то функция на промежутке возрастает (убывает).
Например.
Найти промежутки монотонности функции 
.
Найдём производную 
. Очевидно, что при 
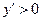, и функция возрастающая, а при 
, и функция убывающая.
Экстремумы функции
Точка 
называется точкой максимума (минимума), если существует такая окрестность этой точки, что для любой точки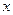 
этой окрестности выполняется неравенство: 
(
). Точки минимума и максимума носят общее название точек экстремума.
Теорема“Необходимый признак экстремума функции одного аргумента”. Если является точкой экстремума, то 
либо 
не существует.
Точки, в которых выполняется необходимое условие, называют критическими.
Например.
Для функции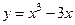 
критическими точками являются 
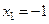и 
, так как 
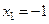при и .
Теорема“Первый достаточный признак экстремума функции одного аргумента”. Если непрерывна в критической точке , дифференцируема в некоторой её окрестности, за исключением быть может самой точки , и при переходе через точку производная функции меняет свой знак с + на -, то является точкой максимума, если производная меняет знак с - на +, то - точка минимума, если производная не меняет знака при переходе через , то не является точкой экстремума.
Например.
Для функци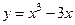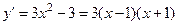и : 
и 
производная меняет свой знак с + на – в точке 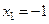и, следовательно, 
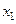является точкой максимума, а в точке производная меняет знак с - на + и 
- точка минимума этой функции.
Рис.1.5.
Теорема «Второй достаточный признак наличия экстремума».
Если в критической точке функции обращаются в ноль не только её первая производная , но и все последующие производные до (n-1) –го порядка включительно 
, а производная n -го порядка существует и отлична от нуля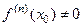 
, то точка будет точкой экстремума, если число n чётное и не будет ею, если n нечетное.
Характер экстремума при чётном n определяется по знаку производной n -го порядка 
: если 
, то -точка минимума, а если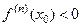 
, то точка максимума.
Например.
Для функции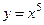 
в критической точке 
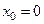, обращаются в 0 
, 
, 
и 
, а 
, поскольку номер отличной от 0 производной нечётный -5, следовательно 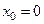не является точкой экстремума.
Следствие. Если 
, а 
, то при 
точка есть точка максимума, а при 
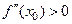
точка минимума.
Для нахождения наибольшего и наименьшего значения функции на отрезке [a,b] надо:
1. Найти критические точки функции.
2. Выбрать из критических точек те, которые принадлежат отрезку [a,b].
3. Вычислить значение функции в выбранных точках и на концах отрезка.
4. Выбрать набольшее и наименьшее значение из полученных значений функции.
Не нашли, что искали? Воспользуйтесь поиском: