Правило Бернулли-Лопиталя для раскрытия неопределенностей

Вычисляя пределы функций, при непосредственной подстановке в функцию значения, к которому стремится 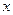, часто получают выражения вида: , по которым нельзя сделать вывода о существовании и значении предела. Эти выражения называются неопределенностями, а нахождение таких пределов – раскрытием неопределенностей.

I. Неопределённости вида и

Теорема Бернулли-Лопиталя. Пусть и дифференцируемы в окрестности точки , за исключением самой точки , и в окрестности точки . Если и являются одновременно либо бесконечно малыми (то есть ) либо бесконечно большими (то есть ) при и при этом существует предел отношения их производных при , то существует и предел отношения самих функций , причем: .

Теорема справедлива и в том случае, если .

Например.

1.

2. , .

3. Иногда правило Лопиталя применяют несколько раз:

.

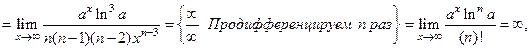
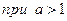II. Неопределённости вида и ()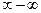

Для вычисления , где - бесконечно малая функция, а - бесконечно большая функция при ( неопределенность ) необходимо преобразовать произведение к виду 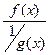( неопределенность ) или к виду ( неопределенность ).

Например.

Для вычисления , где и - бесконечно большие функции при ( неопределенность 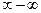) необходимо преобразовать разность к виду и затем рассмотреть неопределенность типа . Если , то 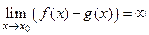. Если же , то является неопределенностью типа , рассмотренной выше.

Например. .

III. Неопределенности вида 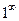, и

К неопределенностям таких типов приходят при вычислении предела выражения . Для их раскрытия выражение логарифмируют и вычисляют предел , который является неопределенностью и сводится к или .

Например.

Вычислить предел: .

Прологарифмируем выражение:

Вычислим предел логарифма:

Так как 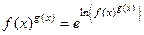, то

Формула Тейлора

Формула Тейлора ставит в соответствие функции многочлен, значение которого в точке и n его производных совпадают со значением 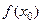и её производных в той же точке.

Теорема. Пусть функция (n+1) -раз непрерывно дифференцируема в интервале , тогда для каждой точки и справедлива формула Тейлора:.

где - остаточный член формулы Тейлора в форме Лагранжа.

Теорема позволяет любую функцию, удовлетворяющую условиям теоремы, заменить в окрестности точки многочленом с точностью до бесконечно малой более высокого порядка малости, чем члены многочлена при . Это делает формулу Тейлора удобной для приближенных вычислений.

Например.

Разложить функцию в окрестности точки .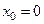

Вычислим производные функции в точке .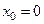

, ; , ;

, ;

, ;

, ;

, .

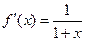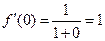Подставим производные и 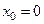в формулу Тейлора:

Окончательно,

Не нашли, что искали? Воспользуйтесь поиском: