Определение функции многих переменных

Упорядоченную совокупность n действительных чисел называют точкой и обозначают , а сами числа 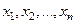называют координатами точки 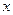. Множество всех таких точек называется арифметическим 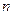-мерным пространством .

Арифметическое 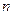- мерное пространство называется 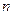- мерным евклидовым пространством, если для любых двух точек 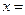() и 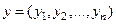принадлежащих , расстояние между ними определяется по формуле: ^.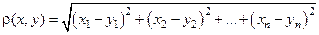

Пусть - некоторая фиксированная точка пространства .

Множество точек 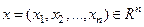, координаты которых удовлетворяют условию: -называется замкнутым 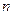- мерным шаром радиуса R с центром в точке .

Множество точек 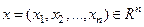таких, что 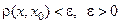называется 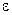-окрестностью точки 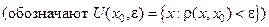. Например, в трехмерном евклидовом пространстве это открытый шар радиуса .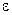

Множество точек 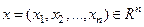, координаты которых заданы как непрерывные функции 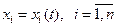, определенные на отрезке называется непрерывной кривой в пространстве . Аргумент 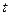называется параметром кривой.

Определение. Если каждой точке множества поставлено в соответствие действительное число 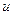, то говорят, что на множестве 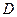задана числовая функция 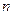- переменных , т.е. 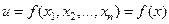. Множество 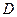называется областью определения функции .

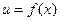В случае n=2, функцию двух переменных чаще обозначают 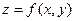и рассматривают как функцию координат точек плоскости xOy. Графиком этой функции является множество точек 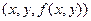, которое задает некоторую поверхность в трехмерном пространстве. Например, 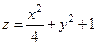- функция двух переменных, ее график - эллиптический параболоид.

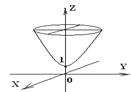
Рис. 2.1.

Например, 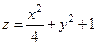- функция двух переменных, ее график - эллиптический параболоид (Рис 2.1.).

В случае функции трех переменных, обозначаемой 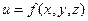, график функции построить невозможно, но о характере поведения можно судить, построив, так называемое, семейство поверхностей уровня, уравнения которых есть 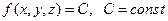. Каждая из таких поверхностей есть множество точек, в которых функция имеет постоянное значение. Например,

для функции 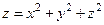поверхностями уровня будут концентрические сферы с центром в начале координат (Рис 2.2.).

Рис. 2.2.

Не нашли, что искали? Воспользуйтесь поиском: