Выпуклость и вогнутость графика функции

График функции называется выпуклым (вогнутым) на отрезке [a,b], если точки графика функции лежат ниже (выше) любой касательной, проведенной к графику функции на отрезке [a,b] (Рис. 1.6). Точки, в которых график дифференцируемой функции меняет выпуклость на вогнутость и наоборот, называют точками перегиба. (Рис. 1.7.).

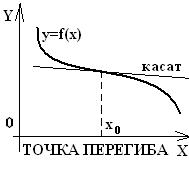
Рис.1.6. Рис.1.7.

Теорема “Признак выпуклости и вогнутости графика функции”. Если функция дважды дифференцируема на промежутке и , то график функции на промежутке выпуклый (вогнутый).

Теорема “Необходимый признак точки перегиба графика функции”. Если функция дважды непрерывно дифференцируема в точке , и точка является точкой перегиба, то .

Теорема “Достаточный признак точки перегиба графика функции”. Если дифференцируема в точке и дважды дифференцируема в ее окрестности и при переходе через точку меняет знак, то является точкой перегиба.

Например.

Для функции 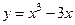вторая производная , если . Очевидно, что при переходе через меняет свой знак с минуса на плюс, следовательно, 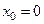является точкой перегиба и кроме того, при график функции выпуклый, а при вогнутый.

Не нашли, что искали? Воспользуйтесь поиском: