Предел и непрерывность функции многих переменных

Пусть дана функция , определенная на множестве .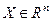

Определение. Число называется пределом функции при стремлении точки к точке по множеству , если для любого числа существует такое число , что для всех точек , таких что выполняется неравенство: .

Обозначают:

В силу данного определения основные теоремы о пределах, справедливые для функции одной действительной переменной, справедливы и для функции 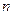переменных.

Например.

Определение. Функция называется непрерывной в точке , если она определена в некоторой окрестности этой точки и существует предел функции при равный значению функции в точке :

.

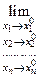
Замечание. Из непрерывности функции по совокупности аргументов вытекает ее непрерывность и по каждому из аргументов в отдельности, но обратное неверно.

Если функция непрерывна в каждой точке области, то она называется непрерывной в этой области. Точки области определения, в которых функция теряет непрерывность, называются точками разрыва функции. В силу данных определений основные теоремы о непрерывных функциях, справедливые для функции одной переменной, справедливы и для функций n переменных.

Не нашли, что искали? Воспользуйтесь поиском: