Определенный интеграл как предел интегральной суммы

Если функция f(x) определена на отрезке 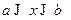и 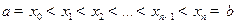- произвольное разбиение этого отрезка на n частей, то интегральной суммой функции f(x) на[ a,b ] называется сумма вида

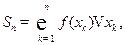
где 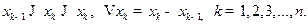Геометрически S_n есть алгебраическая сумма площадей прямоугольников, имеющих основания и высоты .

Если определенная на отрезке [ a,b ] функция f(x) такова, что существует конечный предел последовательности интегральных сумм S_n при условии, что наибольшая из разностей стремится к нулю, причем этот предел не зависит ни от способа разбиения отрезка [ a,b ] на части [ x_k-1,x_k ], ни от выбора точек 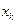на этих отрезках, то функция f(x) называется интегрируемой на отрезке [ a,b ], а сам предел называется определенным интегралом от функции f(x) в пределах от a до b и обозначается символом 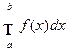. Таким образом,

Непрерывная, либо имеющая конечное число точек разрыва первого рода на отрезке [ a,b ] функция f(x) интегрируема на этом отрезке.

Геометрически определенный интеграл представляет собой алгебраическую сумму площадей фигур, ограниченных графиком функции y= f(x), осью Ox и прямыми x=a и x=b, причем площади, расположенные выше оси Ox, входят в эту сумму со знаком «плюс», а площади, расположенные ниже оси Ox, -со знаком «минус» (Рис. 3.1.).

Рис. 3.1.

4.3.2. Формула Ньютона – Лейбница

Если F(x) – одна из первообразных непрерывной на [ a,b ] функции f(x), то справедлива формула Ньютона – Лейбница:

Эта формула позволяет использовать для вычисления определенных интегралов известные методы нахождения неопределенных интегралов.

Например.

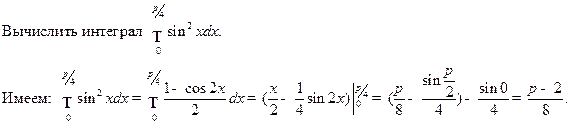
Не нашли, что искали? Воспользуйтесь поиском: