Метод интегрирования по частям. Если - дифференцируемые функции, то справедлива следующая формула интегрирования по частям:

Если - дифференцируемые функции, то справедлива следующая формула интегрирования по частям:

или в краткой записи

.

Основные типы интегралов, берущихся по частям
Тип интеграла	u(x)	v(x)dx	Примечание
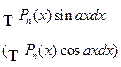
	Pn(x)	sinaxdx	Формула интегрирования по частям применяется столько раз, какова степень многочлена Pn(x)
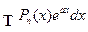
	Pn(x)	eaxdx	Формула интегрирования по частям применяется столько раз, какова степень многочлена Pn(x)
		Pn(x)dx	Избавляемся под знаком интеграла от обратной функции и сводим интеграл к интегралу от рациональной дроби
		Pn(x)dx
	sinbx (eax)	eaxdx (sinxdx)	Формулу применяем дважды, приходим к тому же самому интегралу и из полученного равенства выражаем исходный интеграл

Например.

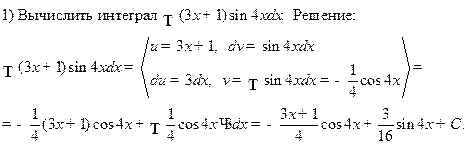
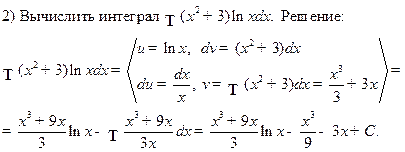
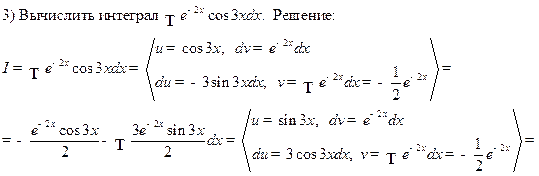
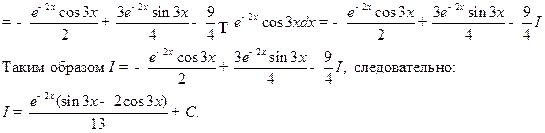
Не нашли, что искали? Воспользуйтесь поиском: