
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчетно-графическая работа. Задания
1. Найти пределы, не используя правило Лопиталя (табл. 1).
2. Найти производные первого порядка явно заданных функций
(табл. 2, а), б), в)) и производную второго порядка (табл. 2, г)).
3. Найти производную первого порядка (для нечетных вариантов) и второго порядка (для четных вариантов) неявно заданной функции (табл. 3).
4. Найти производную первого порядка (для четных вариантов) и второго порядка (для нечетных вариантов) параметрически заданной функции (табл. 4).
5. Выполнить задание на исследование функции (табл. 5).
6. Найти частные производные первого порядка для явно и неявно заданных функций многих переменных (табл. 6).
7. Исследовать на экстремум функцию двух переменных (табл. 7).
Пример выполнения контрольной работы №3. Вариант №0
№ 1. Найти пределы, не используя правило Лопиталя:
А)  ; Б)
; Б)  ; В)
; В)  .
.
№2. Найти производные явно заданных функций:
А) 
 ?
?
Б) 
 ?
?
В) 
 ?
?
Г) 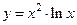
 ?
?
№3. Найти вторую производную неявно заданной функции 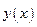 :
:

 ?
?
№4. Найти вторую производную параметрически заданной функции 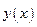 :
:
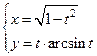
 ?
?
№5. Найти точки экстремума и точки перегиба функции  .
.
Указать промежутки монотонности, промежутки выпуклости и вогнутости графика функции.
№6. Найти частные производные первого порядка функции многих переменных:

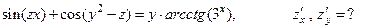
№7. Исследовать функцию на экстремум: 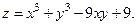
Решение варианта №0.
Задание № 1.
Найти пределы, не пользуясь правилом Лопиталя:
А)  ; Б)
; Б)  ; В)
; В)  .
.
Решение:

 . При подстановке
. При подстановке 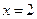 получаем неопределенность «
получаем неопределенность « ». Следовательно,
». Следовательно, 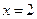 - корень многочленов в числителе и знаменателе. Разложим их на множители:
- корень многочленов в числителе и знаменателе. Разложим их на множители: 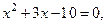 по теореме Виета
по теореме Виета 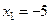
 .
.
Следовательно,  .
.
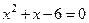 , по теореме Виета
, по теореме Виета 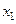
 ,
,  .
.
Получаем  .
.
Тогда:  .
.
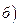

 .
.
При подстановке  получаем неопределенность «
получаем неопределенность « ». Применим формулу
». Применим формулу
понижения степени в знаменателе  и умножим числитель и знаменатель на
и умножим числитель и знаменатель на 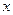 :
:
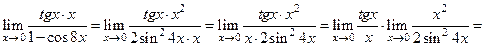

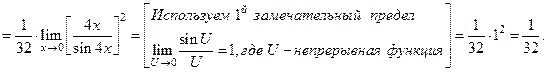
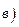
 . При подстановке
. При подстановке 
 получаем неопределенность
получаем неопределенность  . Преобразуем подпредельное выражение так, чтобы можно было воспользоваться вторым замечательным пределом:
. Преобразуем подпредельное выражение так, чтобы можно было воспользоваться вторым замечательным пределом:  , где
, где 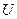 - некоторая непрерывная функция.
- некоторая непрерывная функция.


Ответ:  ,
, 
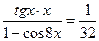 ,
, 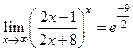 .
.
Задание №2
Найти производные явно заданных функций:
а) 
 ?
?
б) 
 ?
?
в) 
 ?
?
г) 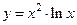
 ?
?
Решение:
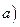
 .
.
Воспользуемся правилами дифференцирования и таблицей производных основных элементарных функций.



= 

 .
.
Воспользуемся правилами дифференцирования и формулой производной для сложной функции  .
.


 .
.



Данная функция является степенно-показательной. Применим формулу логарифмического дифференцирования  :
:
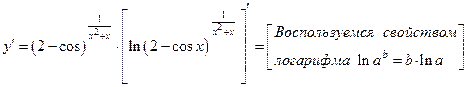

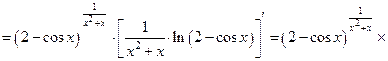

 =
=  .
.

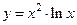
Для нахождения второй производной необходимо найти первую производную.


Задание № 3.
Найти вторую производную неявно заданной функции 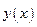 :
: 
Решение: Продифференцируем по 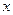 правую и левую части уравнения, определяющего неявно заданную функцию, считая что
правую и левую части уравнения, определяющего неявно заданную функцию, считая что  неизвестная функция:
неизвестная функция:
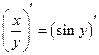 ;
; 
Выразим 
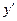 :
: 
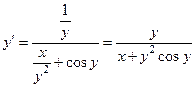
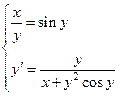 - первая производная неявно заданной функции.
- первая производная неявно заданной функции.
Продифференцируем полученную первую производную повторно:
 ,
,  .
.
Подставим 
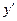 в
в  :
:

Таким образом, 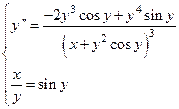 - искомая вторая производная.
- искомая вторая производная.
Задание №4.
Найти вторую производную параметрически заданной функции 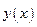 :
:
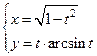
Решение:
Для нахождения второй производной необходимо прежде найти первую производную по формуле 

Получаем 
 -первая производная данной функции.
-первая производная данной функции.
Найдем вторую производную по формуле: 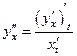
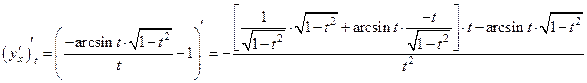
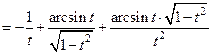 .
.

 .
.
Ответ: 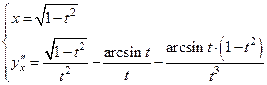 , где
, где  -искомая вторая производная.
-искомая вторая производная.
Задание №5.
Найти точки экстремума и точки перегиба функции  .
.
Указать промежутки монотонности, промежутки выпуклости и вогнутости графика функции.
Решение:
Заметим, что область допустимых значений аргумента:  . Для отыскания точек экстремума найдём первоначально критические точки функции:
. Для отыскания точек экстремума найдём первоначально критические точки функции: 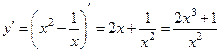 ,
,
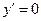 при
при 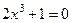 , т. е. при
, т. е. при 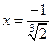 ,
,  - не существует при
- не существует при  .
.
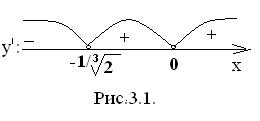
Очевидно, что при переходе через точку 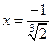 первая производная меняет свой знак с «-» на «+». А при переходе через точку
первая производная меняет свой знак с «-» на «+». А при переходе через точку  не меняет знака. Значит, функция убывает на интервале
не меняет знака. Значит, функция убывает на интервале  ; возрастает на интервалах
; возрастает на интервалах 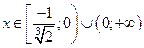 и точка минимума
и точка минимума 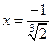 , локальный минимум:
, локальный минимум:
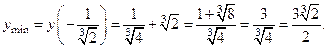
Для нахождения точек перегиба найдём вторую производную данной функции:

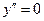 при
при  ,
,  .
.
 - не существует при
- не существует при  .
.

При переходе через точку  вторая производная меняет свой знак с «+» на «-». А при переходе через точку
вторая производная меняет свой знак с «+» на «-». А при переходе через точку  с «-» на «+».
с «-» на «+».
Таким образом, график функции выпуклый на интервале  , вогнутый на интервалах
, вогнутый на интервалах  и имеет две точки перегиба
и имеет две точки перегиба  и
и  .
.
Ответ:  - точка экстремума,
- точка экстремума,  ,
, 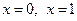 - точки перегиба.
- точки перегиба.
Функция: возрастает на интервалах 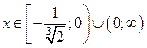 ,
,
убывает на интервале  .
.
График функции: выпуклый на интервале 
 ,
,
Вогнутый 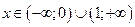 .
.
Задание №6.
Найти частные производные первого порядка функции многих переменных:
а) 
б) 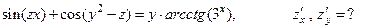
Решение: а) 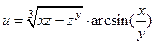 - функция трёх переменных
- функция трёх переменных  . При нахождении частной производной
. При нахождении частной производной 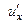 функции
функции  по переменной
по переменной 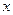 , считаем, что
, считаем, что  являются константами:
являются константами:
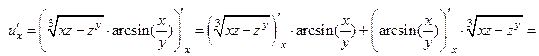
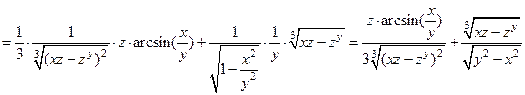 .
.
Аналогично, при нахождении частной производной  функции
функции  по переменной
по переменной  , считаем, что
, считаем, что  являются константами:
являются константами:
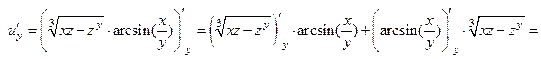


Теперь, при нахождении частной производной  считаем, что
считаем, что 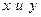 являются константами:
являются константами:

б) Для отыскания частных производных неявно заданной функции двух переменных  используют формулы:
используют формулы: 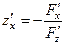 и
и  .
.
Так как  , то следовательно,
, то следовательно,
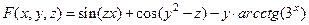
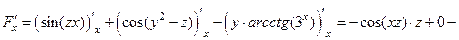
 .
.

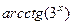 .
.
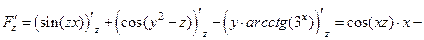
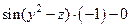 .
.
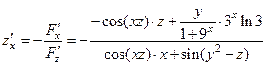 ,
,
 .
.
Задание №7.
Исследовать функцию  на экстремум.
на экстремум.
Решение: Найдём стационарные точки функции: 
 .
.
Следовательно, 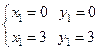 , А(0,0) и В(3,3) - стационарные точки.
, А(0,0) и В(3,3) - стационарные точки.
Вычислим частные производные второго порядка:
 тогда
тогда  .
.
Согласно достаточному признаку наличия экстремума в точке для функции двух переменных получим:
· в точке А(0,0):  , следовательно точка А не является точкой экстремума.
, следовательно точка А не является точкой экстремума.
· в точке В(3,3):  и
и  , следовательно точка В является точкой минимума.
, следовательно точка В является точкой минимума.
 .
.
Ответ: 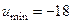 в точке
в точке 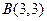 .
.
Варианты заданий расчетно-графической работы.
Таблица 1. Варианта задания 1.
| Вариант | а) | б) | в) |
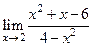
| 
| 
| |
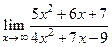
| 
| 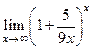
| |

| 
| 
| |

| 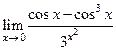
| 
| |
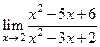
| 
| 
| |

| 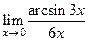
| 
| |
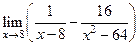
| 
| 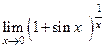
| |
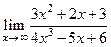
| 
| 
| |

| 
| 
| |

| 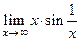
| 
| |

| 
| 
| |
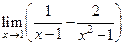
| 
| 
| |
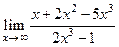
| 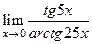
| 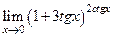
| |
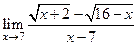
| 
| 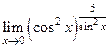
| |

| 
| 
| |

| 
| 
| |

| 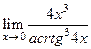
| 
| |

| 
| 
| |
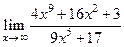
| 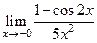
| 
| |

| 
| 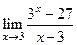
|
Таблица 2. Варианты задания 2.
| № | А) | Б) | В) | Г) |

| 
| 
| 
| |

| 
| 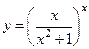
| 
| |

| 
| 
| 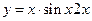
| |

| 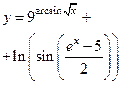
| 
| 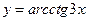
| |

| 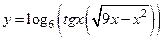
| 
| 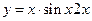
| |

| 
| 
| 
| |

| 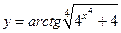
| 
| 
| |
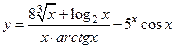
| 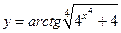
| 
| 
| |
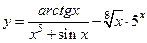
| 
| 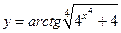
| 
| |
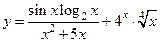
| 
| 
| 
| |
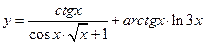
| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
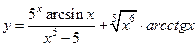
| 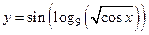
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 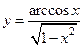
| |
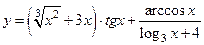
| 
| 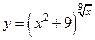
| 
| |

| 
| 
| 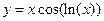
| |
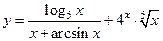
| 
| 
| 
| |
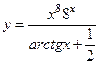
| 
| 
| 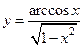
|
Таблица 3. Варианты задания 3.
| Вариант |
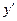 ? ?
| Вариант |
 ? ?
|

| 
| ||

| 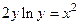
| ||

|
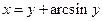
| ||
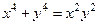
| 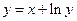
| ||

|

| ||

| 
| ||

| 
| ||
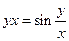
| 
| ||

| 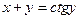
| ||

| 
|
Таблица 4. Варианты задания 4.
| Вариант |  -? -?
| Вариант | 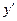 -? -?
|
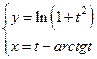
| 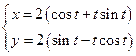
| ||
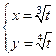
| 
| ||

| 
| ||

| 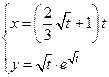
| ||

| 
| ||

| 
| ||
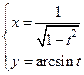
| 
| ||

| 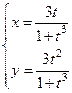
| ||

| 
| ||

| 
|
Таблица 5. Варианты задания 5.
| Вариант | |
Найти промежутки выпуклости, вогнутости и точки перегиба графика функции: 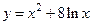 . .
| |
Найти промежутки монотонности и точки экстремума функции:
 . .
| |
Найти наибольшее и наименьшее значения функции:  на отрезке на отрезке  . .
| |
Найти промежутки выпуклости, вогнутости и точки перегиба графика функции: 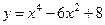 . .
| |
Найти наибольшее и наименьшее значения функции 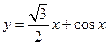 на отрезке на отрезке  . .
| |
Найти промежутки монотонности и точки экстремума функции
 . .
| |
Найти промежутки выпуклости, вогнутости и точки перегиба графика функции  . .
| |
Найти наибольшее и наименьшее значения функции 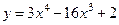 на отрезке на отрезке 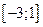 . .
| |
Найти точки экстремума и промежутки монотонности графика функции  . .
| |
Найти промежутки выпуклости, вогнутости и точки перегиба графика функции  . .
| |
Найти наибольшее и наименьшее значения функции  на отрезке на отрезке  . .
| |
Найти промежутки монотонности и экстремумы функции  . .
| |
Найти промежутки монотонности и экстремумы функции  . .
| |
Найти наибольшее и наименьшее значения функции  на отрезке на отрезке  . .
| |
Найти промежутки монотонности и экстремумы функции  . .
| |
Найти промежутки выпуклости, вогнутости и точки перегиба функции  . .
| |
Найти наибольшее и наименьшее значения функции 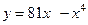 на отрезке на отрезке 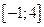 . .
| |
Найти промежутки выпуклости, вогнутости и точки перегиба графика функции  . .
| |
Найти точки перегиба, промежутки выпуклости вогнутости графика функции 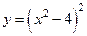 . .
| |
Найти наибольшее и наименьшее значения функции 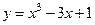 на отрезке на отрезке 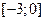 . .
|
Таблица 6. Варианты задания 6.
| Вариант | а) | б) |
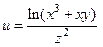
| 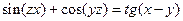
| |

| 
| |
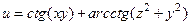
| 
| |

| 
| |

| 
| |
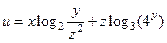
| 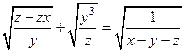
| |

| 
| |

| 
| |
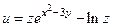
| 
| |
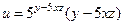
| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 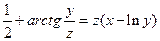
| |

| 
| |
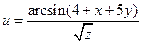
| 
|
Таблица 7. Варианты задания 7.
| Вариант | Вариант | ||
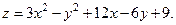
| 
| ||

| 
| ||
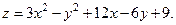
| 
| ||

| 
| ||

| 
| ||

| 
| ||
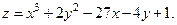
| 
| ||

| 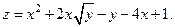
| ||

| 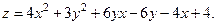
| ||
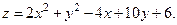
| 
|
Не нашли, что искали? Воспользуйтесь поиском: