Интегрирование рациональных дробей. Интеграл от рациональной дроби , где Pm(x) и Qn(x) многочлены степени m и n соответственно всегда вычисляется в элементарных функциях

Интеграл от рациональной дроби , где P_m(x) и Q_n(x) многочлены степени m и n соответственно всегда вычисляется в элементарных функциях. Алгоритм вычисления:

а) если 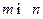(т.е. дробь неправильная), то делим числитель на знаменатель (уголком) и выделяем целую часть и правильную рациональную дробь;

б) знаменатель дроби раскладываем на простейшие множители;

в) представляем правильную рациональную дробь в виде суммы элементарных дробей с неопределенными коэффициентами (вид разложения определяется разложением знаменателя на простейшие множители).

Например:

г) находим неопределенные коэффициенты, для этого домножаем обе части равенства на общий знаменатель, после чего приравниваем коэффициенты при одинаковых степенях x в левой и правой частях равенства; либо придаем х произвольные значения, в частности, удобно полагать х равным действительным корням знаменателя (на практике целесообразно комбинировать оба этих метода). Получаем необходимое число уравнений для нахождения всех неопределенных коэффициентов;

д) вычисляем интегралы от целой части и элементарных дробей.

Например:

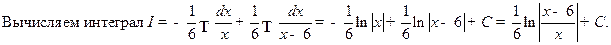
Не нашли, что искали? Воспользуйтесь поиском: