Условный экстремум функции многих переменных

Пусть - функция 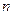независимых аргументов и задано 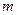уравнений, связывающих аргументы функции ():

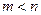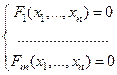. Такие уравнения называются уравнениями связи.

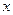Точка , координаты которой удовлетворяют всем уравнениям связи, называется точкой условного максимума (минимума) функции , если существует окрестность точки , для всех точек которой, удовлетворяющих уравнениям связи, выполняется неравенство: ().

Например, пусть задана функция трех переменных 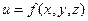и уравнение связи 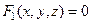. Геометрически это означает, что экстремум функции 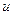ищется среди точек расположенных на поверхности, задаваемой уравнением 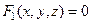. Если записать еще одно уравнение связи 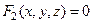, то геометрически это будет означать, что экстремум функции 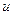разыскивается на кривой линии, которая является пересечением поверхности 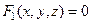и поверхности .

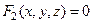Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа:

,

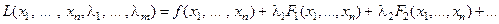
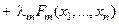где 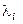- постоянные, так называемые множители Лагранжа .

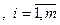Таким образом, возможные точки условного экстремума находят из системы n+m уравнений:

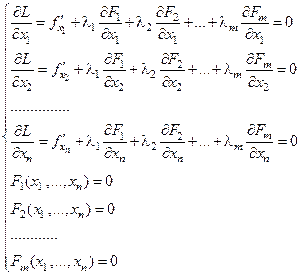
Наличие или отсутствие экстремума в найденных стационарных точках устанавливают с помощью достаточных признаков, применяя их к функции Лагранжа.

Задача на условный экстремум возникает, в частности, тогда, когда необходимо найти наибольшее и наименьшее значение функции на границе какой-либо области.

Для отыскания глобального экстремума функции многих переменных заданной в замкнутой области 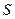надо:

1) Найти все стационарные точки функции в этой области и точки, в которых она не дифференцируема.

2) Вычислить значение функции во всех этих точках.

3) Используя уравнения связи, которые задают границы области, составить функцию Лагранжа и решить задачу на условный экстремум функции, то есть найти максимальное и минимальное значение функции на границе области.

4) Выбрать наибольшее и наименьшее значение среди набора чисел, полученных в пунктах 2 и 3.

Не нашли, что искали? Воспользуйтесь поиском: