
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Площадь плоской фигуры
Площадь фигуры, ограниченной графиком непрерывной функции  , двумя прямыми x=a и x=b и осью Ox (такую фигуру называют криволинейной трапецией, Рис. 3.2.) вычисляется по формуле
, двумя прямыми x=a и x=b и осью Ox (такую фигуру называют криволинейной трапецией, Рис. 3.2.) вычисляется по формуле
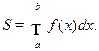
Площадь фигуры, ограниченной графиками непрерывных функций 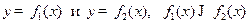 и двумя прямыми x=a и x=b (Рис. 3.3.), вычисляется по формуле
и двумя прямыми x=a и x=b (Рис. 3.3.), вычисляется по формуле
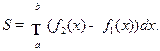
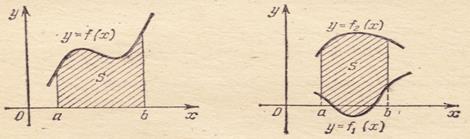
Рис. 3.2. Рис. 3.3.
Например.
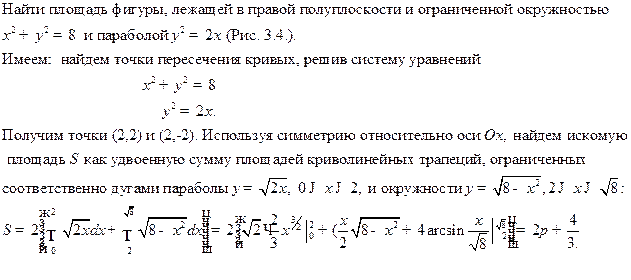
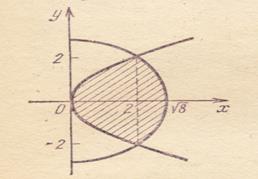
Рис. 3.4.
Если фигура ограничена кривой, имеющей параметрические уравнения x=x(t), y=y(t), прямыми x=a, x=b и осью Ox, то площадь ее вычисляется по формуле
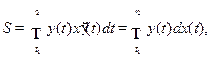
где пределы интегрирования находятся из уравнений a=x(t1), b=x(t2) (y(t) 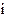 0 на отрезке [ t1, t2 ]).
0 на отрезке [ t1, t2 ]).
Эта формула применима также для вычисления площади фигуры, ограниченной замкнутой кривой (изменение параметра t от t1 до t2 должно соответствовать обходу контура по часовой стрелке).
Например.

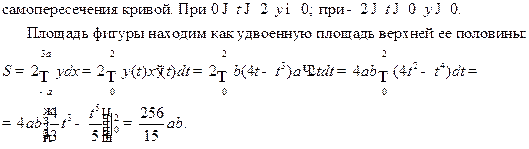
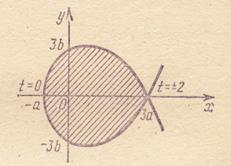
Рис. 3.5.
Площадь фигуры, ограниченной графиком непрерывной функции 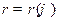 и двумя лучами
и двумя лучами 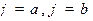 , где
, где 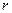 и
и  - полярные координаты, или площадь криволинейного сектора, ограниченного дугой графика функции
- полярные координаты, или площадь криволинейного сектора, ограниченного дугой графика функции 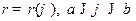 , вычисляется по формуле
, вычисляется по формуле
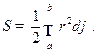
Например.
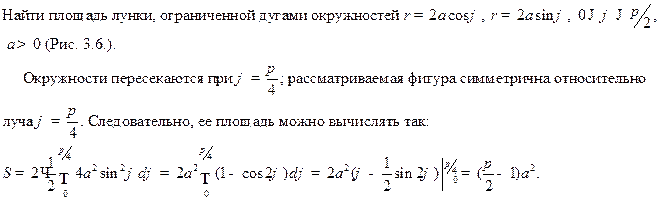
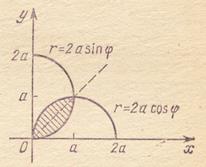
Рис. 3.6.
Длина дуги кривой
Если гладкая кривая задана уравнением y=f(x), то длина l ее дуги равна
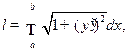
где a и b - абсциссы концов дуги.
Если же кривая задана параметрическими уравнениями 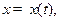
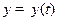
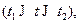 то
то
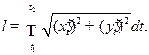
Аналогично выражается длина дуги пространственной кривой, заданной параметрическими уравнениями 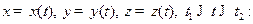

Если задано полярное уравнение гладкой кривой 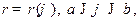 то
то
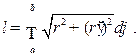
Например.
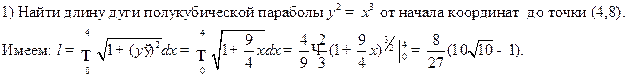

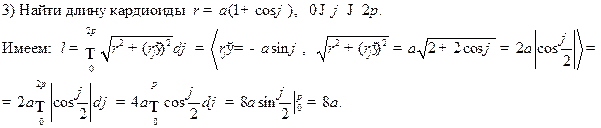
Не нашли, что искали? Воспользуйтесь поиском: