Несобственные интегралы второго рода

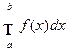Если функция f(x) непрерывна при и , то интеграл называют несобственным интегралом второго рода и по определению полагают

Если F(x) первообразная для f(x) и существует конечный предел , то несобственный интеграл называется сходящимся, если этот предел не существует, то – расходящимся.

Аналогично определяется несобственный интеграл в случае .

Если подынтегральная функция неограничена в любой окрестности некоторой внутренней точки с интервала интегрирования, то полагают

Признаки сходимости для несобственных интегралов второго рода аналогичны признакам из п. 4.1. (за исключением необходимого признака сходимости).

При использовании предельного признака сравнения, в случае несобственных интегралов второго рода, обычно используются интегралы вида

которые сходятся при и расходятся при .

Например.

.

Кратные интегралы

Двойной интеграл

Пусть D замкнутая область на плоскости в декартовой прямоугольной системе координат Oxy. Пусть z и z=f(x, y) – произвольная функция, определенная и непрерывная в этой области. Разобьем область D на n -непересекающихся областей D_i , площади которых обозначим через . В каждой области D_i возьмем произвольную точку M_i (x_i, y_i) и составим сумму

,

которую назовем интегральной суммой.

Определение. Если существует конечный предел последовательности интегральных сумм при и стремлении к нулю максимального из диаметров частичных областей D_i , который не зависит от способа разбиения области на частичные области D_i и выбора точек M_i, то этот предел называется двойным интегралом от функции по области D и обозначается

, т.е.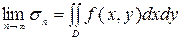

Теорема существования двойного интеграла. Если функция непрерывна в области , то двойной интеграл существует.

Геометрический смысл двойного интеграла.

Рис. 1

Величина двойного интеграла от функции в области равна объему цилиндрического тела, ограниченного сверху поверхностью , снизу замкнутой областью плоскости , с боков - цилиндрической поверхностью, образующая которой параллельна оси (Рис.1), т.е. .

В частности, если , то двойной интеграл будет равен площади области D:

.

Не нашли, что искали? Воспользуйтесь поиском: