Вычисление двойного интеграла. Пусть область D определяется неравенствами:

Пусть область D определяется неравенствами:

и при этом, всякая прямая, параллельная оси Oy пересекает границу области D не более чем в двух точках (Рис. 3), тогда вычисление двойного интеграла от функции в области D сводится к вычислению, так называемого, повторного интеграла по формуле:

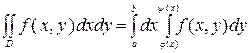(1).

В формуле (1) сначала вычисляется внутренний интеграл по переменной y,считая при этом х величиной постоянной

.

Затем вычисляется внешний интеграл по переменной х.

Рис. 3 Рис.4

Если область интегрирования есть

и при этом, всякая прямая, параллельная оси Ox пересекает границу области D не более чем в двух точках (Рис. 4), тогда двойной интеграл вычисляется через повторный интеграл по формуле:

(2).

Замечание 1.

Рис.5

Если область интегрирования более сложная, чем в описанных выше случаях, то ее можно разбить на несколько непересекающихся частей, удовлетворяющих указанным условиям, при помощи прямых параллельных координатным осям. Затем применить свойство аддитивности. Например, область, изображенную на Рис.5, можно разбить на три области. Тогда

Замечание 2. Пределы интегрирования внешнего интеграла в повторном интеграле всегда постоянны. Пределы интегрирования внутреннего интеграла, в общем случае, будут функциями той переменной, по которой вычисляется внешний интеграл.

Пример.

Вычислить двойной интеграл , где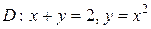

Решение. Область интегрирования D ограничена прямой 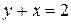и параболой , проходящей через начало координат, с осью симметрии Oy (Рис. 6).

Рис.6

Определим точки пересечения графиков функций. Для того решим систему: Þ

Имеем две точки пересечения: . Любая прямая, проходящая через внутренние точки отрезка параллельно оси Оy пересекает границу области D в двух точках: в точке входа , в которой и в точке выхода , в которой . Таким образом, область интегрирования D можно задать неравенствами: 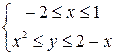. Тогда по формуле (1) получаем:

.

Сначала вычисляем внутренний интеграл по y, считая х постоянной величиной

.

Далее вычисляем внешний интеграл

Ответ:

Не нашли, что искали? Воспользуйтесь поиском: