
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Пример 1. Какое количество кислорода выпустили из баллона емкостью , если при этом показания манометра на баллоне изменилось от до
Пример 1. Какое количество кислорода выпустили из баллона емкостью  , если при этом показания манометра на баллоне изменилось от
, если при этом показания манометра на баллоне изменилось от  до
до  , а температура понизилась от
, а температура понизилась от  до
до  ?
?
Дано:  ;
;  ;
;  ;
;  ;
;  .
.
Манометр показывает разность давлений между давлением в баллоне и атмосферным, поэтому, чтобы найти давления газа в баллоне  и
и 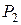 , прибавим к показаниям манометра величину атмосферного давления, равную
, прибавим к показаниям манометра величину атмосферного давления, равную  .
.
 (техническая атмосфера)=
(техническая атмосфера)=  .
.
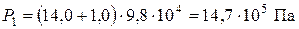 ;
;  .
.
Найти:  .
.
Решение. Масса выпущенного из баллона газа  равна разности между начальной массой
равна разности между начальной массой  кислорода в баллоне и его конечной массой
кислорода в баллоне и его конечной массой 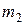 :
:
 . (1)
. (1)
Так как условия, при которых кислород находится в баллоне, не слишком сильно отличаются от нормальных, газ можно считать идеальным. Поэтому, воспользовавшись уравнением состояния идеального газа, запишем его для начального и конечного состояний газа в баллоне:
 ,
,  . (2)
. (2)
Из уравнений  ,
,  получим:
получим:
 . (3)
. (3)
Подставив числовые значения величин, входящих в формулу  , получим:
, получим:
 .
.
Ответ:  .
.
Пример 2. Определить среднюю арифметическую скорость молекул идеального газа, плотность которого при давлении  составляет
составляет 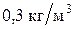 .
.
Дано:  ;
;  .
.
Найти:  .
.
Решение. Для решения задачи воспользуемся уравнением молекулярно–кинетической теории идеальных газов:
 , (1)
, (1)
где  – концентрация молекул;
– концентрация молекул;  – масса одной молекулы;
– масса одной молекулы;  – средняя квадратичная скорость молекул.
– средняя квадратичная скорость молекул.
Учитывая, что  ,
, 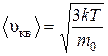 ,
,
получаем  .
.
Отсюда выразим среднюю арифметическую скорость через среднюю квадратичную:
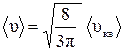 . (2)
. (2)
Среднюю квадратичную скорость найдем из уравнения (1), предварительно его преобразовав. Введем в уравнение (1) плотность газа:
 ,
,
где  – масса газа;
– масса газа;  – его объем;
– его объем;  – число всех молекул газа,
– число всех молекул газа,  – масса молекулы газа,
– масса молекулы газа,  – концентрация молекул.
– концентрация молекул.
Тогда уравнение  примет вид:
примет вид:
 .
.
Отсюда
 . (3)
. (3)
Подставив выражение  в формулу
в формулу  , получим выражение для средней арифметической скорости через заданные физические величины:
, получим выражение для средней арифметической скорости через заданные физические величины:
 . (4)
. (4)
Выполним вычисления, подставив числовые значения физических величин в  :
:
 .
.
Ответ:  .
.
Пример 3. В закрытом сосуде при температуре  и давлении
и давлении  находится
находится  водорода и
водорода и  гелия. Считая газы идеальными, определить удельный объем смеси.
гелия. Считая газы идеальными, определить удельный объем смеси.
Дано:  ;
;  ;
; 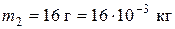 ;
;  ;
;  .
.
Найти:  (удельный объём – объем единицы массы вещества, т.е.
(удельный объём – объем единицы массы вещества, т.е.  ).
).
Решение. Согласно закону Дальтона, давление  смеси газов равно сумме парциальных давлений:
смеси газов равно сумме парциальных давлений:
 . (1)
. (1)
Воспользовавшись уравнением состояния идеального газа – уравнением Менделеева-Клапейрона, запишем его для состояния каждой из газовых компонент, заключенных в объеме смеси  :
:
 и
и  ,
,
где  ,
, 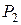 – парциальные давления.
– парциальные давления.
Найдя отсюда парциальные давления  и
и 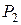 и подставив в уравнение
и подставив в уравнение  , получим:
, получим:

или
 . (2)
. (2)
Из соотношения  выразим объем сосуда, в котором находится смесь газов:
выразим объем сосуда, в котором находится смесь газов:
 .
.
Удельный объем смеси
 . (3)
. (3)
Подставляя числовые значения физических величин, входящих в  , получаем:
, получаем:
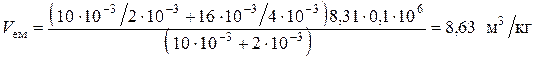 .
.
Ответ:  .
.
Пример 4. Найти относительное число молекул  со скоростями, отличающимися от наиболее вероятной не более, чем на
со скоростями, отличающимися от наиболее вероятной не более, чем на  .
.
Дано:  .
.
Найти:  .
.
 Решение: Изобразим график функции Максвелла распределения молекул по скоростям. Площадь тонированной полоски на рис. 5 – это вероятность (относительное число молекул) того, что скорости молекул лежат в интервале скоростей, равном
Решение: Изобразим график функции Максвелла распределения молекул по скоростям. Площадь тонированной полоски на рис. 5 – это вероятность (относительное число молекул) того, что скорости молекул лежат в интервале скоростей, равном  :
:
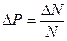 . (1)
. (1)
Решение задачи сводим к нахождению площади полоски. Так как  , то площадь полоски можно найти приближенно, как площадь прямоугольника. Из рис. 5 получаем:
, то площадь полоски можно найти приближенно, как площадь прямоугольника. Из рис. 5 получаем:
 ,
, 
где  , поскольку на
, поскольку на  отклонения могут быть как в одну, так и в другую сторону;
отклонения могут быть как в одну, так и в другую сторону;  – значение функции Максвелла для той скорости, около которой выбран интервал
– значение функции Максвелла для той скорости, около которой выбран интервал  (по условию задачи скорость, около которой выбран интервал
(по условию задачи скорость, около которой выбран интервал  , есть наивероятнейшая
, есть наивероятнейшая 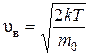 ).
).
Распределение молекул по скоростям выражается уравнением:
 .
. 
Выражение  подставляем в
подставляем в  , с учетом, что
, с учетом, что  ,а
,а  , получаем:
, получаем:

Ответ:  .
.
Пример 5. Используя функцию распределения молекул идеального газа по относительным скоростям  , определить число молекул, скорости
, определить число молекул, скорости  которых меньше
которых меньше  наиболее вероятной скорости, если в объеме газа содержится
наиболее вероятной скорости, если в объеме газа содержится  молекул.
молекул.
Дано:  ,
,  ;
;  ;
;  ;
;  .
.
 Найти:
Найти:  .
.
Решение. В условии задачи речь идет о молекулах, скорости которых заключены в интервале от  до
до  (рис. 6). Таким образом, условие применимости закона распределения скоростей
(рис. 6). Таким образом, условие применимости закона распределения скоростей

или в относительных скоростях
 ,
, 
заключающееся в том, что  или
или  , здесь не выполняется. Поэтому от уравнения в форме
, здесь не выполняется. Поэтому от уравнения в форме  надо перейти к дифференциальной форме этого закона:
надо перейти к дифференциальной форме этого закона:
 ,
, 
где  – полное число молекул в объеме газа,
– полное число молекул в объеме газа, 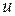 – относительная скорость
– относительная скорость  .
.
Полное число  молекул, относительные скорости которых лежат в заданном интервале от
молекул, относительные скорости которых лежат в заданном интервале от  до
до 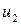 , найдем, интегрируя правую часть
, найдем, интегрируя правую часть  в этих пределах:
в этих пределах:
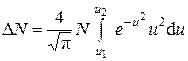 .
. 
Уравнение  является общей формой записи закона распределения скоростей молекул, справедливой для любых интервалов скоростей. Учитывая, что относительная скорость
является общей формой записи закона распределения скоростей молекул, справедливой для любых интервалов скоростей. Учитывая, что относительная скорость  и что в нашей задаче
и что в нашей задаче  и
и  , получим:
, получим:  и
и 
 . Так как интеграл
. Так как интеграл  в конечном виде не берется, воспользуемся методом приближенного интегрирования. Для этого разложим подынтегральную функцию
в конечном виде не берется, воспользуемся методом приближенного интегрирования. Для этого разложим подынтегральную функцию  в ряд Маклорена:
в ряд Маклорена:

Так как  , то
, то  . Тогда выражение
. Тогда выражение  примет вид:
примет вид:
 .
. 
Проинтегрируем выражение  по
по 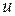 в пределах от
в пределах от  до
до  , найдем:
, найдем:
 .
.
Выполним вычисления  , подставив в конечную формулу числовые значения физических величин:
, подставив в конечную формулу числовые значения физических величин:
 .
.
Ответ:  .
.
 Пример 6. Узкую трубку длины
Пример 6. Узкую трубку длины 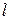 , один торец которой запаян, вращают с постоянной угловой скоростью
, один торец которой запаян, вращают с постоянной угловой скоростью  в горизонтальной плоскости вокруг вертикальной оси
в горизонтальной плоскости вокруг вертикальной оси 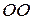 , проходящей через открытый конец трубки, (рис. 7). Это происходит в газе, состоящем из молекул массы
, проходящей через открытый конец трубки, (рис. 7). Это происходит в газе, состоящем из молекул массы  , при температуре
, при температуре  . Концентрация молекул у открытого конца трубки равна
. Концентрация молекул у открытого конца трубки равна  . Найти концентрацию молекул у запаянного торца.
. Найти концентрацию молекул у запаянного торца.
Дано:  ;
;  ;
; 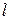 ;
;  .
.
Найти:  .
.
Решение: Газ в трубке находится в поле центробежных сил инерции  (имеется в виду система отсчета, связанная с вращающейся трубкой).
(имеется в виду система отсчета, связанная с вращающейся трубкой).
Из механики известно, что консервативная сила равна градиенту потенциальной энергии частицы, взятой с обратным законом  . В проекциях на направление перемещения
. В проекциях на направление перемещения  :
:
 ,
,
где  – частная производная потенциальной энергии по
– частная производная потенциальной энергии по 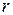 .
.
Воспользуемся последним соотношением для расчета потенциальной энергии молекулы:
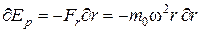 ,
,
 ,
,
 ,
,
где  – потенциальные энергии, соответствующие открытому и закрытому торцам трубки.
– потенциальные энергии, соответствующие открытому и закрытому торцам трубки.
Будем считать, что  , где
, где 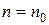 , тогда
, тогда
 .
.
Используя функцию Больцмана распределения молекул по потенциальным энергиям, получим концентрацию молекул у запаянного торца:

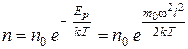 .
.
Ответ:  .
.
Пример 7. Какое количество теплоты теряется ежечасно через окно за счет теплопроводности воздуха, заключенного между рамами? Площадь каждой рамы  , расстояние между рамами
, расстояние между рамами 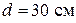 . Температура помещения
. Температура помещения  , температура наружного пространства
, температура наружного пространства  . Диаметр молекул воздуха принять равным
. Диаметр молекул воздуха принять равным  , температуру воздуха между рамами считать равной среднему арифметическому температур помещения и наружного пространства. Давление воздуха нормальное
, температуру воздуха между рамами считать равной среднему арифметическому температур помещения и наружного пространства. Давление воздуха нормальное  .
.
 Дано: воздух (состоит в основном из двухатомных молекул);
Дано: воздух (состоит в основном из двухатомных молекул); 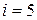 (число степеней свободы);
(число степеней свободы);  ;
;  ;
;  ;
;  ;
;  ;
; 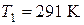 ;
;  ;
;  ;
; 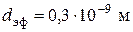 ;
;  .
.
Найти:  .
.
Решение. Согласно закона Фурье количество теплоты, переносимое через площадь 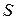 за время
за время  :
:
 ,
, 
где  – коэффициент теплопроводности;
– коэффициент теплопроводности;  – градиент температуры (градиент температуры – вектор, направленный в сторону убыли температуры, рис. 8).
– градиент температуры (градиент температуры – вектор, направленный в сторону убыли температуры, рис. 8).
По молекулярно кинетической теории коэффициент теплопроводности для газов равен
 ,
, 
где  – средняя арифметическая скорость молекул;
– средняя арифметическая скорость молекул;  – средняя длина свободного пробега молекул;
– средняя длина свободного пробега молекул;  – плотность газа;
– плотность газа;  – удельная теплоемкость газа при постоянном объеме
– удельная теплоемкость газа при постоянном объеме  .
.
Проведем расчет коэффициента теплопроводности, рассчитывая каждую физическую величину, входящую в выражение  отдельно.
отдельно.
1. Средняя арифметическая скорость молекул газа, заключенного между рамами, определяется выражением:
 ,
,
где  – температура воздуха между рамами (по условию задачи эта температура равна среднему арифметическому температур
– температура воздуха между рамами (по условию задачи эта температура равна среднему арифметическому температур  и
и  т.е.
т.е.  );
);  – молярная масса воздуха.
– молярная масса воздуха.
Проведем расчет  :
:
 .
. 
2. Средняя длина свободного пробега молекул газа определяется выражением:
 ,
,
где  – эффективный диаметр молекулы,
– эффективный диаметр молекулы, 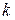 – постоянная Больцмана
– постоянная Больцмана  .
.
Проведем расчет  :
:
 .
. 
3. Плотность газа выразим из уравнения состояния идеального газа, учтя, что  :
:
 или
или  ,
,
откуда
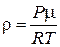 .
.
Проведем расчет  :
:
 .
. 
4. Удельная теплоемкость газа при  :
:
 .
.
Проведем расчет:
 .
. 
Подставив в  числовые значения
числовые значения  ,
,  ,
,  ,
,  из
из  ,
,  ,
,  ,
,  , получим числовое значение коэффициента теплопроводности воздуха для условий, приведенных в данном примере:
, получим числовое значение коэффициента теплопроводности воздуха для условий, приведенных в данном примере:
 .
.
Найдем градиент температуры:
 .
.
Подставив в  числовые значения
числовые значения  ,
,  ,
, 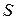 ,
,  , получим:
, получим:
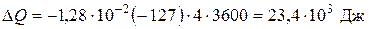 .
.
Ответ:  .
.
Пример 9. Баллон емкостью  с кислородом при давлении
с кислородом при давлении 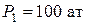 и температуре
и температуре  нагревается до
нагревается до  . Какое количество теплоты при этом поглощает газ?
. Какое количество теплоты при этом поглощает газ?
Дано: 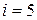 (газ О2 двухатомный),
(газ О2 двухатомный), 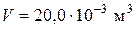 ;
;  ;
;  ;
; 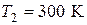 .
.
Найти: Q.
Решение. Поскольку коэффициенты теплового расширения для твердых тел значительно меньше (приблизительно в сто раз), чем для газа, в условиях данной задачи можно пренебречь расширением баллона и считать процесс нагревания газа изохорным.
Количество теплоты можно найти двумя способами, применяя первое начало термодинамики или формулу, определяющую теплоемкость тела.
Первый способ. Применим к рассматриваемому газу первое начало термодинамики. Поскольку при изохорном процессе газ не совершает работы, то первое начало примет вид:
 ,
,
т.е. все сообщенное газу тепло идет на приращение его внутренней энергии. Используя уравнение газового состояния  , выразим внутреннюю энергию газа:
, выразим внутреннюю энергию газа:
 .
.
Отсюда изменение внутренней энергии при переходе газа из состояния 1 в состояние 2 равно
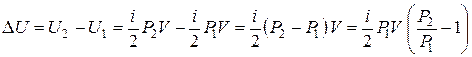 .
.
Заменяя по закону Шарля для изохорного процесса отношение давлений  отношением абсолютных температур
отношением абсолютных температур  , получим
, получим
 .
. 
Второй способ. Из определения молярной теплоемкости  следует, что элементарное количество теплоты, сообщенное телу при повышении температуры на
следует, что элементарное количество теплоты, сообщенное телу при повышении температуры на  , равно
, равно
 .
. 
Число молей  найдем из уравнения Менделеева – Клапейрона для начального состояния газа (
найдем из уравнения Менделеева – Клапейрона для начального состояния газа ( ):
):
 .
.
Так как газ нагревается при постоянном объеме, то  . Подставив выражения для
. Подставив выражения для  и
и  в
в  , получим:
, получим:
 .
. 
Проинтегрировав (3) и учтя при этом, что все величины 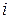 ,
,  ,
,  ,
,  – постоянные, получим полное количество теплоты, поглощенное газом при нагревании от
– постоянные, получим полное количество теплоты, поглощенное газом при нагревании от  до
до  :
:
 ,
, 
что совпадает с выражением  .
.
Выполним вычисления:
 .
.
Ответ:  .
.

Пример 10. Один моль идеального газа из жестких двухатомных молекул совершает цикл Карно. Температура нагревателя 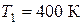 . Найти КПД цикла, если при адиабатическом сжатии затрачивается работа
. Найти КПД цикла, если при адиабатическом сжатии затрачивается работа  .
.
Дано: 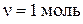 ; газ двухатомный;
; газ двухатомный; 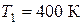 ;
;  .
.
Найти:  (КПД) цикла Карно (рис. 9).
(КПД) цикла Карно (рис. 9).
Решение. В адиабатическом процессе  работа, совершаемая газом
работа, совершаемая газом
 .
.
Работа, совершаемая над газом  , тогде
, тогде

 .
. 
Выполним преобразования выражения  , домножим и разделим на
, домножим и разделим на  :
:
 .
. 
Величина в круглых скобках выражения  – КПД цикла Карно
– КПД цикла Карно  . Поэтому выражение
. Поэтому выражение  примет вид:
примет вид:
 .
. 
Из  следует, что
следует, что
 .
.
Поскольку число молей  ,
,  – молярная теплоемкость при
– молярная теплоемкость при  , то
, то
 ,
,
где 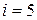 (газ двухатомный, молекула жесткая).
(газ двухатомный, молекула жесткая).
Выполним вычисления:
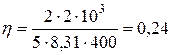 .
.
Ответ:  .
.
 Пример 11. Идеальный трехатомный газ совершает цикл, состоящий из двух изохор и двух изобар (рис. 10). Определить КПД
Пример 11. Идеальный трехатомный газ совершает цикл, состоящий из двух изохор и двух изобар (рис. 10). Определить КПД  цикла, если
цикла, если  ,
,  ;
; 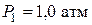 ,
,  .
.
Дано: газ идеальный, трехатомный;  – число степеней свободы;
– число степеней свободы;  ;
;  ;
;  ;
;  .
.
Решение. Изображенный на рис.10 цикл состоит из четырех последовательно протекающих процессов. Коэффициент полезного действия тепловой машины, работающей по замкнутому циклу:
 ,
, 
где  – работа, совершаемая рабочим веществом, (в данном случае газом), в течение цикла;
– работа, совершаемая рабочим веществом, (в данном случае газом), в течение цикла;  – количество теплоты, полученное газом в течение цикла;
– количество теплоты, полученное газом в течение цикла;  – отдаваемое тепло.
– отдаваемое тепло.
Выясним, на каких участках газ получает тепло, а на каких – отдает.
1. Участок 1 – 2. Объем  сохраняется, при этом давление газа увеличивается от
сохраняется, при этом давление газа увеличивается от  до
до 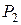 . Так как при изохорном процессе давление пропорционально абсолютной температуре, повышение давления вызвано повышением температуры. Следовательно, газ при этом получает количество теплоты
. Так как при изохорном процессе давление пропорционально абсолютной температуре, повышение давления вызвано повышением температуры. Следовательно, газ при этом получает количество теплоты 
 .
.
Согласно первому закону термодинамики исходное количество теплоты 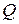 , требуемое при нагревании, равно
, требуемое при нагревании, равно
 .
.
Так как в изохорическом процессе работа газом не совершается  , то все тепло идет на изменение внутренней энергии:
, то все тепло идет на изменение внутренней энергии:
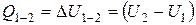 .
. 
2. Участок 2 – 3. Давление 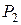 газа сохраняется, объем увеличивается от
газа сохраняется, объем увеличивается от  до
до  . Так как при изобарическом процессе объем газа пропорционален температуре, то увеличение объема вызвано повышением температуры. Следовательно, и здесь газ получает количество теплоты
. Так как при изобарическом процессе объем газа пропорционален температуре, то увеличение объема вызвано повышением температуры. Следовательно, и здесь газ получает количество теплоты 
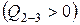 . В изобарическом процессе количество теплоты идет на изменение внутренней энергии и на совершение работы самим газом
. В изобарическом процессе количество теплоты идет на изменение внутренней энергии и на совершение работы самим газом  .
.
Работа газа в изобарическом процессе на участке 2 – 3:
 .
. 
Количество теплоты, полученное газом на участке 2 – 3:
 .
. 
3. Участок 3 – 4. Процесс идет изохорно  , давление уменьшается от
, давление уменьшается от 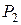 до
до  , понижается и температура. В этом процессе газ отдает количество теплоты
, понижается и температура. В этом процессе газ отдает количество теплоты 
 .
.
4. Участок 4 – 1. Процесс идет изобарно  , газ сжимается от объема
, газ сжимается от объема  до
до  , температура газа понижается. Следовательно, здесь газ отдает некоторое количество теплоты
, температура газа понижается. Следовательно, здесь газ отдает некоторое количество теплоты 
 . В этом изобарном процессе над газом совершается работа:
. В этом изобарном процессе над газом совершается работа:
 .
. 
Теперь приступаем к вычислению КПД 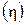 цикла по формуле
цикла по формуле  .
.
Учитывая, что газ получает теплоту на участках 1 – 2 и 2 – 3, то количество теплоты  , сообщенное газу при нагревании:
, сообщенное газу при нагревании:
 .
. 
Подставив в  вместо
вместо 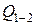 и
и  их выражения
их выражения  и
и  , получим:
, получим:
 .
. 
Изменение внутренней энергии  при переходе газа из состояния 1 в состояние 3
при переходе газа из состояния 1 в состояние 3

или на основании уравнения состояния газа – уравнения Менделеева-Клапейрона  :
:
 .
. 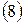
Подставив в  вместо
вместо  выражение
выражение 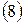 , получим:
, получим:
 .
. 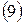
Работа газа, совершаемая им на участках 2 – 3 и 4 – 1, равна, согласно  и
и  :
:
 .
. 
Эту же формулу работы можно получить сразу, если учесть, что работа газа, совершенная за цикл, численно равна площади фигуры, ограниченной замкнутой линией – графиком цикла в системе координат  . В данном случае эта работа равна площади прямоугольника 1 – 2 – 3 – 4.
. В данном случае эта работа равна площади прямоугольника 1 – 2 – 3 – 4.
Наконец, подставляя в  выражения
выражения  и
и  из
из 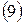 и
и  , найдем КПД цикла:
, найдем КПД цикла:
 .
. 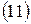
Выполним вычисления КПД, подставив в 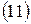 числовые значения физических величин в единицах СИ:
числовые значения физических величин в единицах СИ:
 .
.
Ответ:  .
.
Пример 12. Один моль идеального газа, состоящего из одноатомных молекул, находится в сосуде при температуре  . Как и во сколько раз изменится статистический вес (термодинамическая вероятность) этой макросистемы, если ее нагреть изохорически на
. Как и во сколько раз изменится статистический вес (термодинамическая вероятность) этой макросистемы, если ее нагреть изохорически на  ?
?
Дано: газ одноатомный,  (число степеней свободы),
(число степеней свободы), 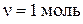 ;
;  ; процесс изохорический
; процесс изохорический  .
.
Найти:  .
.
Решение. Воспользуемся формулой Больцмана связи энтропии 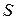 и статистического веса
и статистического веса  макросистемы:
макросистемы:
 ,
,
где 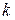 – постоянная Больцмана.
– постоянная Больцмана.
Исходя из этой формулы, имеем:
 .
. 
Из соотношения  видно, что решение сводится к нахождению приращения энтропии макросистемы
видно, что решение сводится к нахождению приращения энтропии макросистемы  . Как известно, изменение энтропии выражается формулой:
. Как известно, изменение энтропии выражается формулой:
 .
. 
Согласно первому началу термодинамики для изохорического процесса  количество теплоты
количество теплоты  идет только на изменение внутренней энергии макросистемы:
идет только на изменение внутренней энергии макросистемы:
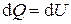 .
. 
Изменение внутренней энергии идеального газа для одного моля  :
:
 .
. 
Перепишем выражение  с учетом
с учетом  и
и  в виде:
в виде:
 ,
, 
где температура конечного состояния  .
.
Из сопоставления формул  и
и  получим:
получим:
 ,
, 
где  – число Авогадро.
– число Авогадро.
Так как по условию задачи  , то, разложив функцию
, то, разложив функцию  в ряд, в первом приближении можно принять, что
в ряд, в первом приближении можно принять, что  , тогда выражение
, тогда выражение  примет вид:
примет вид:
 .
.
Выполним вычисления натурального логарифма отношения вероятностей:
 .
.
Из последнего соотношения находим:
 .
.
Эта величина чудовищно огромная даже при таких скромных изменениях температуры.
Ответ:  .
.
Пример 13. Найти давление, при котором плотность углекислого газа при температуре  окажется равной
окажется равной  .
.
Дано: Газ  , молярная масса которого
, молярная масса которого  ,
,  ,
, 
Найти:  .
.
Решение. Оценим плотность газа, считая его идеальным и находящимся при нормальных условиях  . Для этого воспользуемся уравнением состояния идеального газа
. Для этого воспользуемся уравнением состояния идеального газа  . Решая его относительно плотности, получим:
. Решая его относительно плотности, получим:
 (1)
(1)
Отсюда
 .
.
Так как плотность газа по условию задачи во много раз больше плотности его при нормальных условиях, то, очевидно, что газ необходимо рассматривать как реальный, параметры которого связаны уравнением состояния Ван-дер-Вальса
 .
.
Решив его относительно давления  , получим:
, получим:
 .
.
На основании определения плотности  и, имея в виду, что
и, имея в виду, что  , получим:
, получим:
 .
. 
Взяв из таблиц в приложениях значения постоянных  и
и  для углекислого газа
для углекислого газа  ,
,  и
и  , выполним вычисления давления по формуле
, выполним вычисления давления по формуле  :
:

Расчет давления по формуле состояния идеального газа  дает результат:
дает результат:

Различие в давлениях весьма значительное.
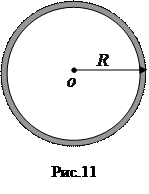 Ответ:
Ответ: 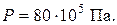
Пример 14. Какую работу против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь радиусом  ? Чему равно избыточное давление внутри пузыря? Коэффициент поверхностного натяжения мыльной воды
? Чему равно избыточное давление внутри пузыря? Коэффициент поверхностного натяжения мыльной воды  .
.
Дано: 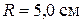 ,
,  .
.
Найти:  ;
;  .
.
Решение. Мыльный пузырь представляет собой очень тонкую пленку мыльной воды приблизительно сферической формы. Эта пленка имеет две поверхности – наружную и внутреннюю, рис. 11. Пренебрегая толщиной пленки и считая радиусы обеих сфер одинаковыми, найдем их общую площадь:
 .
. 
Так как до образования пузыря поверхность мыльной воды, из которой он выдут, очень мала, то можно считать, что соотношение  выражает изменение (увеличение) площади
выражает изменение (увеличение) площади  поверхности мыльной воды.
поверхности мыльной воды.
Увеличение поверхности жидкости на  приводит к приросту поверхностной энергии
приводит к приросту поверхностной энергии  :
:
 ,
, 
где s – коэффициент поверхностного натяжения.
Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии  . Таким образом, из
. Таким образом, из  и
и  получим:
получим:
 .
. 
Избыточное давление внутри пузыря, вызванное кривизной поверхности, т.е. давление, производимое каждой сферической поверхностью, находим по формуле Лапласа:
 ,
,
где  и
и  – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости (для сферы
– радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости (для сферы  );
);  – избыточное давление, производимое одной поверхностью.
– избыточное давление, производимое одной поверхностью.
Таким образом, избыточное (по сравнению с наружным) давление воздуха внутри пузыря, учитывая две сферические поверхности:
 .
. 
Подставив в  и
и  числовые значения, получим:
числовые значения, получим:
 .
.
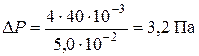 .
.
Ответ:  ,
,  .
.
Пример 15. Вертикальный капилляр привели в соприкосновение с поверхностью воды. Какое количество теплоты выделится при поднятии воды по капилляру? Смачивание считать полным, поверхностное натяжение равно  .
.
Дано: вертикальный капилляр;  – коэффициент поверхностного натяжения.
– коэффициент поверхностного натяжения.
 Найти:
Найти: 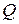 .
.
Решение. Работа  , совершаемая силами поверхностного натяжения при поднятии жидкости, идет на сообщение ей потенциальной и кинетической энергии:
, совершаемая силами поверхностного натяжения при поднятии жидкости, идет на сообщение ей потенциальной и кинетической энергии:
Не нашли, что искали? Воспользуйтесь поиском: