Випадкові величини. Закон розподілу випадкової дискретної величини. Формула Бернуллі, Пуассона.

Випадковою називається величина, яка внаслідок випробування може прийняти те або інше можливе значення, невідоме заздалегідь, але обов язково одне.При багаторазовому проведення досліду в незмінних умовах у загальному випадку будуть отримані різні значення випадкової величини.

Дискретною випадковою величиною називають таку випадкову величину, безліч можливих значень якої скінченне або нескінченне, але рахункове. Приклади: число студентів групи, число похмурих днів у році.
Закон розподілу дискретної випадкової величини – це відповідність між значеннями випадкової величини та їхніми ймовірностями. Закон розподілу можна задати таблично, формулою, графічно. При цьому треба враховувати, що сума ймовірностей повинна дорівнювати 1.

Формули Бернуллі

Якщо виконують n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, а не відбувається з імовірнісю q, де q=1-p, то ймовірність того що подія А настане m разів визначається за формулою Бернуллі

.

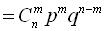
Формула Пуассона (закон рідкісних явищ) дає приблизне значення імовірності в тому випадку, коли число випробувань n велике, а імовірність p=P(А) в кожному з окремих випробувань маленька

.

Значить 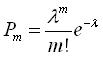, лямбда – деяка позитивна величина, параметр закону Пуассона..

Не нашли, что искали? Воспользуйтесь поиском: