ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Синтез кулачкового механизма с центральным плоским толкателем
На рисунке 2.3 изображена расчетная схема кулачкового механизма с центральным плоским толкателем. Обозначения, принятые на схеме: 
– угол поворота кулачка, 
; 
– минимальный начальный радиус кулачка,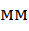 
; 
– угол давления кулачка в точке контакта с толкателем, ; 
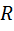– радиус-вектор точки контакта кулачка с толкателем, ; 
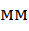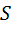– перемещение толкателя, ; 
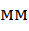– полярный угол радиус-вектора в точке контакта, .
Для построения профиля кулачка используется метод инверсии (обращения движения), при котором вращение подвижного кулачка начинается с определения начального (минимально допустимого) радиуса кулачка 
.
Рис. 2.3. Расчетная схема кулачкового механизма с центральным плоским толкателем:
1 – профиль кулачка; 2 – плоский толкатель
| Рис. 2.4. Схема вычисления начального радиуса кулачка с центральным толкателем |
(допустимое значение для кулачка с плоским толкателем 
. На графике зависимости аналога скорости толкателя от его перемещения 
проведем касательную прямую 
к графику под углом 
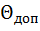к оси перемещения 
(рис. 2.4). Расстояние 
на графике с учетом коэффициента масштаба выражает величину начального радиуса кулачка .
По графику зависимости аналога скорости толкателя от его перемещения находим значения 
и 
в точке касания прямой с графиком. Через тангенс угла 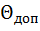вычисляем начальный радиус кулачка 
:
| (2.8) |
| (2.9) |
Построение профиля кулачка производится в полярной системе координат. Для этого задавшись углом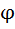 
поворота толкателя, необходимо найти полярный угол 
радиус-вектора 
в точке контакта 
(рис. 2.3).
| (2.10) |
| (2.11) |
| (2.12) |
Длина радиус-вектора в точке контакта находится о формуле:
| (2.13) |
Отмечая точками на графике длины радиус-векторов, вычисленных при соответствующих полярных углах , и обводя их гладкой кривой линией, получим профиль кулачка. Чертеж профиля кулачка выполняется в масштабе.
Не нашли, что искали? Воспользуйтесь поиском: