
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретическая часть. Передаточное отношение является главным кинематическим параметром для любой передачи, в том числе и зубчатой
Передаточное отношение является главным кинематическим параметром для любой передачи, в том числе и зубчатой. Передаточное отношение – это отношение угловой скорости ведущего звена к угловой скорости ведомого звена или его можно выразить через частоту вращения  или число зубьев первого и второго колеса
или число зубьев первого и второго колеса  и
и  соответственно (рис. 1):
соответственно (рис. 1):

| (4.1) |

Рис. 4.1. Рядовой зубчатый механизм
Механизмы, состоящие из двух сопряжённых зубчатых колёс, представляют собой простейший вид зубчатого зацепления. На практике часто необходимо применение значительных передаточных отношений. Для этого применяют несколько последовательно соединённых колёс, которые получили название многоступенчатых зубчатых передач. Многоступенчатые передачи, у которых оси вращения колёс неподвижны, носят название рядового соединения.
В некоторых многоступенчатых зубчатых передачах оси отдельных колёс являются подвижными. Зубчатый механизм, который имеет одну подвижную геометрическую ось в пространстве называют планетарным. Подвижное звено, в котором помещены оси сателлитов называют водилом. Вращающегося вокруг неподвижной оси колесо по которому обкатываются сателлиты называют центральным, подвижным, неподвижное центральное колесо – опорным. Как правило, планетарные механизмы изготовляются соосными (рис. 2). При кинематическом анализе планетарного механизма следует пользоваться формулой:

| (4.6) |
где  – передаточное отношение от колеса 1 к колесу 3 при остановленном водиле;
– передаточное отношение от колеса 1 к колесу 3 при остановленном водиле;  – передаточное отношение планетарного механизма;
– передаточное отношение планетарного механизма;  – угловая скорость колеса 1;
– угловая скорость колеса 1;  – угловая скорость водила
– угловая скорость водила  .
.
| H |
Рис. 4.2. Планетарный механизм
Из этого выражения вычисляем передаточное отношение планетарного механизма путем подстановки числа зубьев:

| (4.7) |
Примечание: знак « » ставится когда зацепление колес внешнее, а знак «+» при внутреннем зацеплении.
» ставится когда зацепление колес внешнее, а знак «+» при внутреннем зацеплении.
Практическая часть
Рядовой механизм
Вычертить зубчатый механизм, выданный преподавателем в стандартном масштабе (М 1:2, 1:2,5, 1:4). Пронумеровать звенья, указать кинематические пары 5-го и 4-го класса. Вычислить степень подвижности по формуле Чебышева  :
:
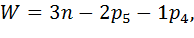
| (4.2) |
где  – число подвижных звеньев;
– число подвижных звеньев;  – количество кинематических пар пятого класса;
– количество кинематических пар пятого класса;  – количество кинематических пар четвертого класса.
– количество кинематических пар четвертого класса.
Измерить диаметр вершин зубьев  и их количество
и их количество  одного из зубчатых колес и вычислить модуль
одного из зубчатых колес и вычислить модуль  :
:

| (4.3) |

| (4.4) |
где  – диаметр вершин зубьев;
– диаметр вершин зубьев;  – число зубьев.
– число зубьев.
Округлить модуль  до стандартного значения по табл. 4.1.
до стандартного значения по табл. 4.1.
Табл. 4.1
Значения модулей  по ГОСТ 9563-60
по ГОСТ 9563-60

| 1 ряд | 1,5 | 2,5 | |||||||
| 2 ряд | 1,75 | 2,25 | 2,75 | 3,5 | 4,5 | 5,5 |
Пример.
М 1:4

Рис. 4.3. Рядовой зубчатый механизм в масштабе
1. Вычисляем степень подвижности  по формуле Чебышева:
по формуле Чебышева:

| |
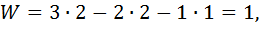
|
где число подвижных звеньев  , так как два вращающихся звена; количество кинематических пар пятого класса
, так как два вращающихся звена; количество кинематических пар пятого класса  , так как два цилиндрических шарнира; число кинематических пар четвертого класса
, так как два цилиндрических шарнира; число кинематических пар четвертого класса 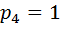 , так как присутствует одна точка касания двух зубьев колес.
, так как присутствует одна точка касания двух зубьев колес.
| P5 |
| P5 |
| P4 |

Рис. 4.4. Рядовой зубчатый механизм с указанием кинематических пар
2. Измерим линейкой диаметр вершин зубьев большого колеса 2: 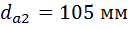 .
.
3. Подсчитаем на механизме число зубьев шестерни 1 и колеса 2:  ,
, 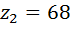 .
.
4. Вычисляем модуль  :
:

| |
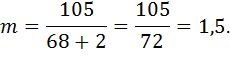
|
5. Сравним полученное значение модуля  с табличным значением по ГОСТ 9563-60 (табл. 4.1).
с табличным значением по ГОСТ 9563-60 (табл. 4.1).
6. Вычисляем передаточное число  :
:
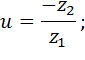
| |

|
Примечание: знак « » ставится когда зацепление колес внешнее, а знак «+» при внутреннем зацеплении.
» ставится когда зацепление колес внешнее, а знак «+» при внутреннем зацеплении.
7. Определяем опытным путем передаточное число, для чего вручную поворачиваем колесо 1 на один полный оборот и замечаем число оборотов 2 колеса. В данном примере колесо 2 повернулось на  оборота. Тогда передаточное число, определенное опытным путем, составит:
оборота. Тогда передаточное число, определенное опытным путем, составит:

|
8. Отклонение между практически определенным и вычисленным передаточным отношением равно:

| (4.5) |

|
Диаметры начальных 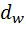 , делительных
, делительных  окружностей, окружностей вершин зубьев (da) и впадин (df) для зубчатых колёс, нарезанных без смещения, вычисляются по формулам, приведённым ниже (точность вычисления делительных диаметров колес до 0,01 мм):
окружностей, окружностей вершин зубьев (da) и впадин (df) для зубчатых колёс, нарезанных без смещения, вычисляются по формулам, приведённым ниже (точность вычисления делительных диаметров колес до 0,01 мм):
начальный шестерни
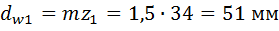 ;
;
начальный колеса
 ;
;
делительной шестерни
 ;
;
делительный колеса
 ;
;
основной шестерни
 ;
;
основной колеса
 ;
;
вершин зубьев шестерни
 ;
;
вершин зубьев колеса
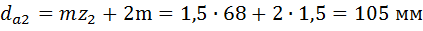 ;
;
впадин зубьев шестерни
 ;
;
впадин зубьев колеса
 ;
;
Планетарный механизм
1. Начертить планетарный механизм в масштабе, пронумеровать колеса, подписать названия звеньев (солнечное колесо, водило, неподвижное колесо, сателлит), вычислить степень подвижности.
| H |
Рис. 4.5. Планетарный механизм
2. Определить передаточное отношение планетарного механизма.
3. Проверить условие соосности.
4. При кинематическом анализе планетарного механизма следует пользоваться формулой:

| (4.6) |
где  – передаточное отношение от колеса 1 к колесу 3 при остановленном водиле;
– передаточное отношение от колеса 1 к колесу 3 при остановленном водиле;  – передаточное отношение планетарного механизма;
– передаточное отношение планетарного механизма;  – угловая скорость колеса 1;
– угловая скорость колеса 1;  – угловая скорость водила
– угловая скорость водила  .
.
Из этого выражения вычисляем передаточное отношение планетарного механизма путем подстановки числа зубьев:

| (4.7) |
Примечание: знак « » ставится когда зацепление колес внешнее, а знак «+» при внутреннем зацеплении.
» ставится когда зацепление колес внешнее, а знак «+» при внутреннем зацеплении.
5. Поворачиваем механизм вручную и проверяем, как сходится практически определенное и вычисленное передаточное отношение.
Не нашли, что искали? Воспользуйтесь поиском: