АААААААААААААААААААААААА

Анықтауыштар. Анықтауыштардың қасиеттері. Анықтама. саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады:

Анықтауыштың қасиеттері. 1-қасиет. Анықтауыштың жолдарын сәйкес бағандармен алмастырсақ, онда оның шамасы өзгермейді. 2-қасиет. Егер анықтауыштың жолдарының орнын ауыстырсақ, онда оның таңбасы өзгереді. 3-қасиет. Егер анықтауыштың кейбір жолының немесе бағанының барлық элементтері нөл болса, онда анықтауыштың шамасы нөлге тең. 4-қасиет. Егер анықтауыштың кейбір жолының элементтерін k санына көбейтсек, онда анықтауыштың шамасы да осы k санына көбейтіледі. Яғни, жолының немесе бағанының ортақ көбейткішін анықтауыштың таңбасының алдына шығаруға болады. 5-қасиет. Егер анықтауыштың екі жолдарының элементтері пропорционал болса, онда анықтауыш нөлге тең. 6-қасиет. Анықтауыштың қайсібір жолының элементтеріне басқа жолдың элементтерін бірдей k санына көбейтіп қосқаннан, анықтауыштың шамасы өзгермейді. 7-қасиет. Егер анықтауыштың қайсібір жолы (бағаны) екі санның қосындысынан тұрса, онда бұл анықтауыш екі анықтауыштың қосындысына тең.

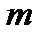Алгебралық сызықтық теңдеулер жүйесі. Үйлесімді, үйлесімсіз, анықталған ж/е анықталмағын жүйелер. Кронекер-Капеллдің теоремасы. Сызықты теңдеулер жүйесiнің негізгі ұғымдары. белгiсiздерi бар теңдеулерден тұратын сызықты жүйе деп, мынандай теңдеулер жүйесiн айтады (1) теңдеулер жүйесiнiң коэффициенттер i, жүйенiң бос мүшелерi, Ең кемiнде бiр шешiмi бар теңдеулер жүйесiн үйлесiмдi,ал шешiмi жоқ теңдеулер жүйесiн үйлесiмсiз деп атайды. Тек қана бiр ғана шешiмi бар жүйенi анықталған, ал бiрден артық шешiмi бар жүйенi анықталмаған деп атайды. Егер барлық болса, онда (1) жүйе бiртектi, ал ең болмағанда бос мүшелердiң бiреуi нөлге тең болмаса ол бiртектi емес деп аталады.

-Анықталмаған интеграл ұғымы. Қасиеттері. Анықтама. (а,в) интервалындағы функцияның алғашқы функцияларының жиынын функцияның анықталмаған интегралы деп атайды да, 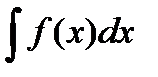символымен белгілейді. Анықталмаған интегралдың қасиеттері.

1. ,

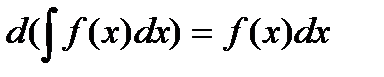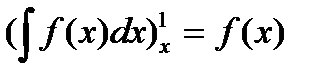
2. 1

3. ,

4. Егер 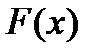функциясы функцияның алғашқы функциясы болса, онда

,

Анықталмаған интегралдарды тікелей интегралдау, алмастыру н/е айнымалыны ауыстыру ж/е бөліктеп интегралдау әдістері. 1) Тікелей интегралдау әдісі. Анықталмаған интегралды оның анықтамасының, қасиеттерінің және интегралдар кестесінің көмегімен интегралдауды тікелей интегралдау әдісі деп атайды. Егер бұл әдіс арқылы интегралдау мүмкін болмаса басқа әдістер қолданылады.

2) Алмастыру немесе айнымалыны ауыстыру әдісі.

.

3)Бөліктеп интегралдау әдісі. , Айнымалылары бойынша біртекті дифференциалдық теңдеулер. Бірінші ретті сызықтық дифференциалдық теңдеулер.

теңдеуін біртекті теңдеуге келтіру үшін , деп алып жаңа және 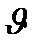айнымалыларын енгізу керек, мұндағы және белгісіз сандарды берілген теңдеу біртекті болатындай етіп табу керек. Яғни олар

теңдеулер жүйесінің шешімі болуға тиіс.

Бірінші ретті сызықтық дифференциалдық теңдеулер. Бірінші ретті сызықты дифференциалдық теңдеу деп, белгісіз фкнкция мен оның туындысы сызықты болатын теңдеуді айтады.

(8)

Мұндағы және 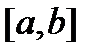кесіндідегі үзіліссіз функциялар. Егер аралығында 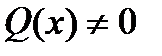болмаса, онда (8) теңдеуді біртексіз ал 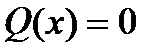болса біртекті сызықты теңдеу деп аталады.

а) Лагранж әдісі (тұрақтыны вариациалау әдісі).

(8) теңдеуге сәйкес біртекті теңдеудің жалпы шешімі , мұндағы с-кез келген тұрақты сан. Тұрақтыны вариациалау әдісі бойынша (8) теңдеудің жалпы шешімін түрінде іздейді.

б) Бернулли әдісі. (8) теңдеудің шешімін екі функцияның көбейтіндісі түрінде іздейді: , онда . және 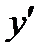-терді (8) теңдеуге қойып өрнегін аламыз. Осы теңдеудің сол жағын топтастырсақ өрнегін аламыз.

Не нашли, что искали? Воспользуйтесь поиском: