Поток векторного поля через поверхность.

При произвольном течении жидкости скорости частиц в общем случае также будут зависеть от их пространственного положения, образуя, следовательно, векторное поле. Векторное поле является векторной функцией векторного аргумента.

Пусть в некоторой области пространства задано векторное поле A(r) и поверхность . Тогда: потоком поля A(r) через поверхность называется величина

Поток через замкнутую поверхность:

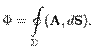
Таким образом, величину потока векторного поля через замкнутую поверхность можно рассматривать как характеристику самого поля. Тогда, векторное поле можно исследовать, помещая пробную замкнутую поверхность в различные области поля и определяя поток Ф.

21.Теорема Остроградского – Гаусса и ее обоснование. Поток векторного поля через замкнутую поверхность.

Теорема Остроградского – Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀:

.

Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностью S произвольной формы. Разобьем замкнутую поверхность на элементарные площадки dS, к каждой из которых проведем вектор нормали.

,

где - элементарный телесный угол, под которым элемент виден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхность S от точечного заряда q, находящегося внутри этой поверхности.

,

так как , то .

Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS1 и dS2, находящиеся внутри телесного угла dΩ равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Общий поток вектора напряженности через замкнутую поверхность равен

Не нашли, что искали? Воспользуйтесь поиском: