ПРЕДЕЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Пусть функция 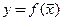определена в некоторой проколотой окрестности точки 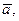где Приведем определение конечного предела функции в конечной точке.

Число называют пределом функции 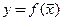в точке и обозначают если для любого сколь угодно малого положительного числа существует положительное число вообще говоря, зависящее от такое, что для всех , удовлетворяющих неравенству выполняется неравенство 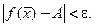Можно доказать, что при стремлении аргумента к точке одновременно, а не последовательно, выполняются условия:

Если функция имеет предел в точке , то предельное значение функции не зависит ни от направления, по которому точка приближается к предельной точке , ни от способа приближения.

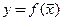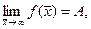По аналогии с функцией одной переменной для функций нескольких переменных можно ввести понятия бесконечного предела в конечной точке, конечного и бесконечного предела на бесконечности. Например, определение конечного предела на бесконечности формулируется так: число называют пределом функции при и обозначают если для любого сколь угодно малого положительного числа существует положительное число вообще говоря, зависящее от такое для всех , удовлетворяющих неравенству 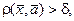выполняется неравенство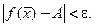

Многие теоремы, описывающие свойства пределов, являются общими для функций одной и нескольких переменных. Ниже приведены наиболее важные из них.

Теорема 1 (о единственности предела). Функция не может иметь более одного конечного предела при (или при .

Говорят, что функция ограничена вблизи точки , если существует положительное число такое, что в некоторой окрестности точки выполнено неравенство .

Теорема 2 (необходимое условие существования конечного предела). Если функция имеет конечный предел А при (или при ), то она ограничена в некоторой проколотой окрестности точки (или для достаточно больших по модулю значений ).

Арифметические свойства пределов

Пусть для функци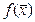й и 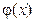существуют конечные пределы А и В соответственно при 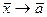. Отметим их арифметические свойства.

1. 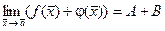– предел суммы двух функций равен сумме пределов.

2. – предел разности двух функций равен разности пределов.

Следствие свойств 1 и 2. Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен такой же сумме пределов этих функций.

3. – предел произведения функций равен произведению пределов.

В частности, постоянный множитель можно выносить за знак предела:

, где .

4. , ( – предел отношения двух функций равен отношению пределов

этих функций, если предел знаменателя не равен нулю.

Эти свойства имеют место и при .

При вычислении пределов функций нескольких переменных можно использовать все приемы вычисления пределов и раскрытия неопределенностей, рассмотренные для функции одной переменной. Однако находить пределы функций нескольких переменных сложнее, чем для функций одной переменной, так как в одномерном случае к предельной точке можно подойти всего лишь с двух сторон: слева и справа, а в многомерном − по бесконечному числу направлений.

Пример 1. Найти

□ Данная функция является элементарной функцией. Вычисление предела связано с раскрытием неопределенности вида :

■

Не нашли, что искали? Воспользуйтесь поиском: