
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определения частных производных и градиента
Рассмотрим функцию двух переменных  определенную в некоторой окрестности точки
определенную в некоторой окрестности точки 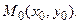 Дадим аргументу
Дадим аргументу  такое частное приращение
такое частное приращение  , сохраняя при этом неизменной координату
, сохраняя при этом неизменной координату  , что точка
, что точка  принадлежит окрестности точки
принадлежит окрестности точки  Разность
Разность 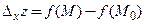 называют соответствующим частным приращением функции по переменной
называют соответствующим частным приращением функции по переменной 
Частной производной  функции
функции 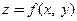 в точке
в точке 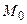 по переменной
по переменной 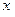 называют предел отношения частного приращения функции
называют предел отношения частного приращения функции 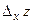 к частному приращению аргумента
к частному приращению аргумента  при стремлении последнего к нулю:
при стремлении последнего к нулю:
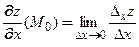 (2)
(2)
Другие обозначения частной производной по переменной 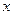 :
:

Из определения частной производной по 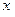 следует, что для ее вычисления нужно выполнить дифференцирование по переменной
следует, что для ее вычисления нужно выполнить дифференцирование по переменной 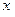 по обычным правилам дифференцирования функций одной переменной, полагая
по обычным правилам дифференцирования функций одной переменной, полагая 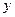 фиксированной величиной (константой).
фиксированной величиной (константой).
Аналогичным образом вводится понятие частной производной 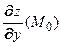 функции по переменной
функции по переменной 
Если частные производные функции 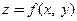 существуют в каждой точке множества
существуют в каждой точке множества 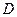 , то они являются функциями переменных
, то они являются функциями переменных 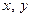 . В этом случае имя и координаты произвольной точки можно не указывать. Обозначения
. В этом случае имя и координаты произвольной точки можно не указывать. Обозначения  и
и 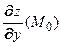 сохраняют для значений частных производных в конкретной точке
сохраняют для значений частных производных в конкретной точке 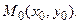
Функция двух переменных 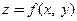 в произвольной точке
в произвольной точке  имеет две частных производных:
имеет две частных производных: 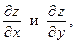 или
или 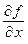 и
и  . Вектор, координаты которого равны частным производным, взятым в указанном порядке, называют градиентом функции:
. Вектор, координаты которого равны частным производным, взятым в указанном порядке, называют градиентом функции:
........... 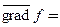
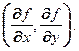 (3)
(3)
Для градиента используют и другое обозначение 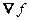 , где
, где 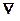 − символ Гамильтона (читается «набла»).
− символ Гамильтона (читается «набла»).
Введенные понятия естественным образом обобщаются на функции нескольких переменных 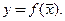 Пусть функция нескольких переменных
Пусть функция нескольких переменных 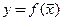 определена в некоторой окрестности точки
определена в некоторой окрестности точки 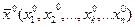 . Разность
. Разность  , где
, где 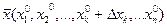 (по сравнению с
(по сравнению с  изменена лишь
изменена лишь 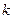 -я координата), называют частным приращением функции по переменной
-я координата), называют частным приращением функции по переменной  , соответствующим частному приращению
, соответствующим частному приращению 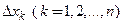 аргумента
аргумента  . Частной производной функции
. Частной производной функции 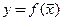 в точке
в точке 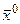 по переменной
по переменной  называют предел отношения частного приращения функции
называют предел отношения частного приращения функции 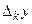 к частному приращению аргумента
к частному приращению аргумента 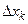 при стремлении последнего к нулю:
при стремлении последнего к нулю:
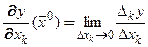 . (4)
. (4)
Другие обозначения частной производной по переменной  в точке
в точке 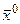 :
:
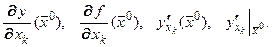
Вектор, координаты которого равны частным производным функции 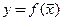 по переменным
по переменным  , называют градиентом функции:
, называют градиентом функции:
........... 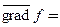
 . (5)
. (5)
Для функций 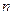 переменных
переменных 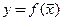 , как и для функций одной переменной, непрерывность функции не является достаточным условием существования конечной частной производной в этой точке. Более того непрерывность функции
, как и для функций одной переменной, непрерывность функции не является достаточным условием существования конечной частной производной в этой точке. Более того непрерывность функции 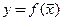 в точке не является и необходимым условием существования конечной частной производной в этой точке: если функция
в точке не является и необходимым условием существования конечной частной производной в этой точке: если функция 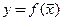 имеет конечную частную производную по переменной
имеет конечную частную производную по переменной  в некоторой точке, то она может быть разрывной в этой точке.
в некоторой точке, то она может быть разрывной в этой точке.
Так, например, функция 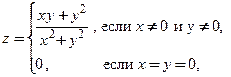 в точке
в точке  имеет частную производную
имеет частную производную 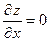 . Действительно, на оси абсцисс при
. Действительно, на оси абсцисс при 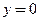 функция тождественно равна нулю:
функция тождественно равна нулю: 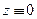 , откуда следует, что
, откуда следует, что  . Рассмотренная функция имеет конечную частную производную в точке
. Рассмотренная функция имеет конечную частную производную в точке  , но тем не менее она разрывна в этой точке.
, но тем не менее она разрывна в этой точке.
Не нашли, что искали? Воспользуйтесь поиском: