НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Рассмотрим функцию определенную в некоторой окрестности точки Функция называется непрерывной в точке , если она удовлетворяет следующим трем условиям:

1) определена в точке (т.е. существует значение );

2) имеет конечный предел при ;

3) этот предел равен значению функции в точке , т.е.

(1)

Назовем значение функции в точке ее частным значением. Тогда называют непрерывнойв точке если предельное значение функции в этой точке равно ее частному значению в этой точке, т.е. имеет место равенство (1).

Саму точку 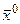называют точкой непрерывности функции 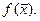Множество всех точек непрерывности образует область непрерывности функции.

Как видим, определения непрерывности в точке функции одной и нескольких переменных совпадают с точностью до обозначений.

Если в точке 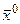не выполнено равенство (1) (функция определена в проколотой окрестности точки 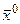,а в точке 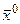не определена, или не существует предел, или нарушено равенство), то точку 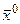называют точкой разрыва и говорят, что функция терпит разрыв в точке У функции нескольких переменных точки разрыва могут образовывать линии или поверхности разрыва. Так, например, элементарная функция терпит разрывы на линиях и поскольку на этих прямых она не определена.

Свойства функций нескольких переменных, непрерывных в точке аналогичны свойствам функций одной переменной, непрерывных в точке.

1. Если функции и непрерывны в точке то их сумма, разность, произведение и частное также непрерывны в точке

2. Если функция 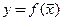непрерывна в точке 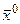и то существует такая окрестность точки 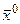, в которой

3. Если функции непрерывны в точке причем а функция непрерывна в точке то сложная функция непрерывна в точке

4. Если функция непрерывна в точке то она ограничена в некоторой окрестности этой точки.

5. Всякая элементарная функция непрерывна в каждой точке области определения.

Функцию называют непрерывной на множестве если она непрерывна в

каждой точке этого множества. При этом используют обозначение:

Кривую называют непрерывной кривой, если координаты точек этой кривой описываются непрерывными функциями параметра .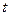

Свойства функции нескольких переменных, непрерывной на замкнутом ограниченном множестве, сходны со свойствами функции одной переменной, непрерывной на отрезке.

Предварим следующую теорему понятиями наибольшего и наименьшего значения функции на множестве. Пусть функция 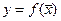определена на множестве D и точки . Если для любой точки выполнено неравенство , то значение функции называют наибольшим значением функции на множестве D. Наибольшее значение функции также называют глобальным максимумом и обозначают 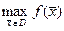, или М. . Если для любой точки выполнено неравенство , то значение функции называют наименьшим значением функции на множестве D. Наименьшее значение функции также называют глобальным минимумом и обозначают , или m.

Теорема 3 (Вейерштрасса). Всякая функция, непрерывная на замкнутом ограниченном множестве, ограничена на этом множестве и достигает на этом множестве своего наибольшего и наименьшего значения.

В качестве примера рассмотрим функцию двух переменных 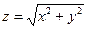, определенную на треугольнике , где . Эта элементарная функция является непрерывной на . Треугольник является замкнутым ограниченным множеством. Значит, согласно теореме 3 Вейерштрасса данная функция ограничена на этом множестве и достигает на нем своего наибольшего и наименьшего значения. Так как значения функции 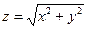равны расстоянию от точки до начала координат в точке : , то наименьшее значение, очевидно, достигается в начале координат =0,, а наибольшее − в наиболее удаленной от начала координат точке : .

Если в рассмотренном примере заменить треугольник на его внутренность: , то задача о наибольшем и наименьшем значениях функции 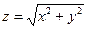решения не имеет, так как в этом случае область D является открытым, а не замкнутым множеством, и условия теоремы 3 не выполняются. Точек, в которых достигаются наименьшее и наибольшее значения, в области D нет.

Не нашли, что искали? Воспользуйтесь поиском: