
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задача 3.1.2 Однофакторный дисперсионный анализ при неслучайном формировании выборок равной численности
Условие: Проведен полевой опыт, в котором изучалось влияние способа внесения гербицида аценита на урожайность пшеницы (Таб. 3.4). При подборе делянок (повторностей) учитывалось плодородие почв.
Установить, достоверны ли различия в урожайности культуры по вариантам опыта. Уровень вероятности суждения 0,95.
Решение:
I. Выдвинем нулевую и альтернативную гипотезы
H 0 : 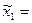

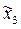 , (между средними величинами в генеральных совокупностях нет достоверных различий, следовательно, способ внесения гербицида не оказывает влияние на уровень урожайности пшеницы)
, (между средними величинами в генеральных совокупностях нет достоверных различий, следовательно, способ внесения гербицида не оказывает влияние на уровень урожайности пшеницы)
H0 : 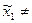

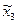 , (между средними величинами в генеральных совокупностях есть достоверные различия, обусловленные влиянием способа внесения аценита).
, (между средними величинами в генеральных совокупностях есть достоверные различия, обусловленные влиянием способа внесения аценита).
Таблица -3.4. Урожайность пшеницы при разных способах внесения аценита, ц /га
| Способ внесения аценита | Повторности | Итого
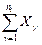
| Средняя
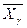
| ||||
| I-под культивацию | 28,8 | ||||||
| II-ленточный | 40,0 | ||||||
| III-под боронование | 38,4 | ||||||
| Итого Σ x i | Σ xij= 536 | 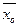 = 35,7 = 35,7
|
2. Определим модель дисперсионного анализа.
Группировочный признак один (способ внесения), следовательно, модель однофакторная. Так как в качестве повторностей рассматривались делянки, имеющие общность условий – одинаковое плодородие почв, то повторности следует признать зависимыми выборками. Таким образом, в нашей задаче три источника вариации:
1) способ внесения аценита (признак, по которому проведена группировка делянок)
2) плодородие почв по повторностям
3) остальные (случайные) факторы
Общий объем вариации равен сумме объемов вариации по источникам варьирования: W общ = W фактора + W повторностей + W остаточная
3. Условные обозначения примем аналогичными для задачи 3.1. Составим таблицу квадратов 3.5. и сделаем в ней вычисления. Для этого все значения, а также суммы значений по строкам и столбцам из таблицы 3.4. возведем в квадрат. Сумма квадратов значений признака по строкам должна быть равна сумме квадратов значений по столбцам. Эта сумма будет составлять сумму квадратов всех значений признака в совокупности Σхĭ 2 = Σхĵ 2 = Σхij 2
Таблица - 3.5. Квадраты значений признаков и их сумм
| Способ внесения | Повторности | Сумма квадратов

| Квадрат суммы
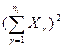
| ||||
| I | |||||||
| II | |||||||
| III | |||||||
Сумма квадратов 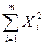
| Σ x2 ij =19586 | 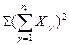 =97600 =97600
| |||||
Квадрат суммы
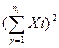
| 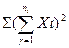 =57548 =57548
| (Σ xij)2 =287296 |
4. Расчет объемов вариации по источникам варьирования проведем по рабочим формулам, рассмотренным в задаче 1.10.
Общий объем вариации урожайности пшеницы равен
 19586-
19586- 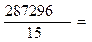 19586 – 19153,0667= 432,9333
19586 – 19153,0667= 432,9333
Объем вариации по вариантам опыта определим по формуле
 =
= 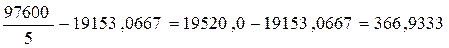
Объем вариации по повторностям равен 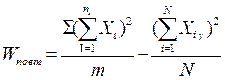 =
=
 = 19182,6667 - 19153,0667 = 29,6
= 19182,6667 - 19153,0667 = 29,6
Объем вариации, обусловленный остальными (случайными) факторами равен согласно правилу разложения объемов вариации разности общего объема вариации и вариации фактора и вариации повторностей
Wост. = Wобщ. - Wфактора – W повт.
432,9333- 366,9333 - 29,6000 = 36,4
5. Рассчитаем число степеней свободы для каждого источника варьирования.
В нашей задаче общее число наблюдений N=15, число групп m = 3, число повторностей n = 5.
Для общего объема вариации число степеней равно
V o= N-1= 15-1 = 14
Число степеней свободы для факторной дисперсии:
V фактора = m-1 = 3-1 = 2
Число степеней свободы для дисперсии повторностей:
V повт = n-1 = 5-1 = 4
Число степеней свободы для остаточной дисперсии:
V ост. = V o - V фактора - V повт =14 – 2 -4= 8
6. Рассчитаем необходимые для дальнейшего анализа дисперсии признака
- Дисперсия по фактору
S факт 2 = 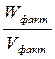 =
= 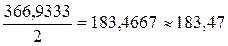
- Дисперсия по повторностям S повт 2 =  =
= 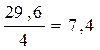
- Дисперсия остаточная S2 ост = 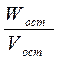 =
= 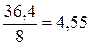
Примечание: Общую дисперсию не вычисляем, так как она не участвует в дальнейшем анализе.
7. Определим фактическое значение F- критерия для каждого источника вариации:
- по фактору Fфакт =  =
= 
- по повторностям Fповт =  =
= 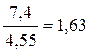
8. Определим теоретические значения критерия F –распределения для каждого источника вариации при заданном уровне значимости 0,05 (приложение 4). Для первого источника вариации в приложении 4 находим по горизонтали в первой строке число степеней свободы для большего среднего квадрата (факторной дисперсии), V1= 2, и опускаем перпендикуляр до строки, указывающей число степеней свободы для меньшего среднего квадрата (остаточной дисперсии) –V2= 8. На пересечении находим значение 4,46.
Для дисперсии повторностей теоретическое значение F находим на пересечении V1=4(по столбцу) и V 2 =8 (по строке), равное 3,84.
9. Результаты решения запишем в таблицу 3.6
Таблица - 3.6. Расчет и анализ дисперсий
| Источник вариации | Объем вариации W | Число степеней свободы V | Дисперсия S2 | Значение F- распределения | |
| Фактическое | Табличное | ||||
| Способ внесения гербицида | 366,9333 | 183,47 | 40,32 | 4,46 | |
| Плодородие почвы | 29,6000 | 7,40 | 1,63 | 3,84 | |
| Случайные факторы | 36,4000 | 4,55 | х | Х | |
| Итого | 432,9333 | х | х | х |
10. Сделаем вывод, с опоставив фактическое и табличное значение критерия F. По первому источнику вариации (способ внесения гербицида) фактическое значение критерия превышает табличное. Так как фактическое значение попадает в критическую область критерия, нулевая гипотеза о равенстве выборочных средних величин в генеральных совокупностях должна быть отвергнута. Принимаем альтернативную гипотезу и применительно к содержанию задачи заключаем, что с вероятностью 0,95 способ внесения гербицида существенно влияет на уровень урожайности культуры.
По второму источнику вариации (плодородие почв) фактическое значение критерия F ниже табличного, следовательно попадает в область допустимых значений. Принимаем нулевую гипотезу как верную и делаем вывод о том, что различия в урожайности по повторностям нельзя признать существенными.
Не нашли, что искали? Воспользуйтесь поиском: