
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Текстовые задачи на движение.
Рассмотрим следующие типы задач на движение:
– одного объекта;
– двух объектов по прямой
а) навстречу;
б) в противоположных направлениях;
в) вдогонку;
– двух объектов по окружности
– одного объекта относительно другого (по реке, по эскалатору, относительно колонны)
– трёх и более объектов.
1. Задачи на движение одного объекта решаются с использованием формулы  , где S – путь, пройденный телом со скоростью v за время t.
, где S – путь, пройденный телом со скоростью v за время t.
Нужно быть внимательным при решении задач на нахождение средней скорости:
1) если речь идёт о средней скорости на равных участках пути, то её можно выразить как среднее арифметическое скоростей на этих участках;
2) если участки пути не равны, то средняя скорость находится по формуле 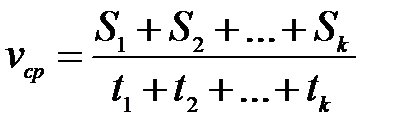 .
.
Пример 1. Первую часть пути велосипедист ехал со скоростью 40 км/ч. Затем путь на 20 км больший он проехал за 1ч 15мин, а последний участок пути, по длине равный первому, он проехал со скоростью 32 км/ч. Найдите длину всего пути, если средняя скорость велосипедиста на всём участке составляла 40 км/ч.
| S | v | t | |
| I | S 1 | v1= 40 | t 1 |
| II | S 2= S 1+20 | v2 | t 2 = 1,25 |
| III | S 3= S 1 | v3= 32 | t 3 |
Воспользуемся формулой  , для этого выразим t 1 и t 3 через S 1.
, для этого выразим t 1 и t 3 через S 1.
 ,
,  , тогда
, тогда  , откуда S 1 = 40 км. Длина всего пути
, откуда S 1 = 40 км. Длина всего пути  =140 км. Ответ 140 км.
=140 км. Ответ 140 км.
При решении задач на движение объекта с отставанием (ускорением) относительно графика важно выяснить, каковы длина пути, где он двигался с отставанием (ускорением) и время опоздания.
Пример 2. Поезд идёт по расписанию из пункта А в пункт В 15 часов. Проехав некоторую часть пути, он снизил скорость в 5 раз и поэтому прибыл в B с опозданием на 11 часов. Если бы поезд до снижения скорости проехал на 150 км больше, то опоздание составило бы 1 час. Найдите расстояние между городами.
Пусть x км/ч – скорость по расписанию. Заметим, что на отрезке пути в 150 км время движения с отставанием составляет 10 часов, поэтому  . Отсюда x = 60, S = 60×15=900 (км).
. Отсюда x = 60, S = 60×15=900 (км).
Не нашли, что искали? Воспользуйтесь поиском: