Задачи на движение одного объекта относительно другого

Пример 5. Пароход плывёт от Киева до Херсона трое суток, а назад – четверо. Найти, сколько суток будет плыть плот от Киева до Херсона.

, отсюда , следовательно, плот от Киева до Херсона будет плыть 24 суток.

Пример 6. Из пункта А одновременно отплыли по течению реки катер и плот. Пройдя км, катер повернул обратно и, пройдя км, встретился с плотом. Найти собственную скорость катера, если скорость течения 4 км/ч.

Заметим, что плот прошёл путь – = 4(км) со скоростью 4 км/ч, значит, он находился в пути 1 час. Катер тоже находился в пути 1 ч. Найдём собственную скорость катера.

1 способ. Можно составить уравнение , из которого найти км/ч.

2 способ. Можно заметить, что относительно плота катер плыл с постоянной скоростью 1 час на одинаковое расстояние и проплыл + = км, где x км – длина пути, пройденного плотом за 0,5 часа, значит, скорость катера 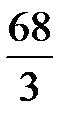км/ч.

Пример 7. Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 15 мин папа заметил пропажу, быстро развернул лодку и они поплыли по течению с той же собственной скоростью. За сколько минут они догонят шляпу?

1 способ. Скорость удаления лодки и шляпы равна 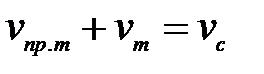; скорость сближения лодки и шляпы равна . Удаление и сближение лодки и шляпы происходило на одно и то же расстояние и с одной и той же скоростью, значит, время движения туда и обратно одинаково. Ответ 15 мин.

2 способ. Относительно шляпы лодка плыла с одинаковой скоростью на одинаковое расстояние, значит, и времени было затрачено одинаково.

Б) по эскалатору

Пример 8. Мальчик сбежал вниз по движущемуся эскалатору и насчитал 30 ступенек. Затем он пробежал вверх по тому же эскалатору и насчитал 150 ступенек. Найти количество ступенек, которое насчитал бы мальчик, спустившись по неподвижному эскалатору.

1 способ. Пусть l – длина эскалатора, – собственная скорость мальчика, – скорость эскалатора, искомое количество ступенек. Составим систему:

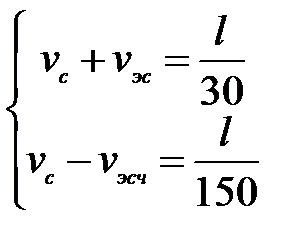, отсюда , значит, количество ступенек равно 50.

2 способ. Пусть x – количество ступенек, которые исчезают (появляются), пока мальчик делает 1 шаг. Тогда количество ступенек эскалатора можно выразить двумя способами: при движении мальчика вниз по движущемуся эскалатору: 30+30 x (те, что он насчитал и те, что спрятались, пока он шагал) и 150–150 x (те, что он насчитал минус лишние, которые появились, пока он шагал).

30+30 x = 150–150 x, отсюда находим , тогда количество ступенек равно 30+30 x = 30+30× =50.

Не нашли, что искали? Воспользуйтесь поиском: