Графический способ решения задач на движение

Введём координатную плоскость, по одной из осей которой от­ложим время t, по другой — путь, пройденный телом S (или выполненную работу). Тогда любая точ­ка этой плоскости с координатами (t, S) будет соответ­ствовать, например, пути S, пройденному объектом за время t, а само движение изобразится некоторой линией в этой плоскости. Если скорость в течение некоторого времени постоянна, движение изображается прямой линией.

Рассмотрим решение предыдущей задачи (пример 10).

Известно, что при движении 2-х объектов с разными скоростями на одно и то же расстояние отношение их скоростей обратно пропорционально отношению времени, затраченного каждым, значит, = ; = , т.е. , ; . Ответ: .

Пример 11 (Задача Льюиса Кэрролла из сборника математических головоломок для школьников) Из двух городов навстречу друг другу вышли одновременно два курьера. После встречи один был в пути 16 часов, а другой – 9 часов. Сколько времени был в пути каждый?

Рис. 1

Обозначим через х ч неизвестный промежуток времени (Рис. 1).

Так как ∆АОР ~ ∆МОК, то .

Так как ∆ВОК ~ ∆ТОР, то .

Таким образом, 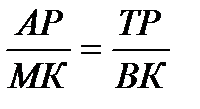, т. е. , откуда х = 12. Тогда время, затраченное на путь каждым:

12 + 16 = 28 (ч); 12 + 9 = 21 (ч).

Ответ: 28 ч, 21 ч.

Пример 14. (задача репетиционного централизованного тестирования 2005 года) Рыболов, охотник и грибник идут в одном направлении с постоянными скоростями. Когда рыболов и охотник находились в одной точке, грибник отстал от них на 220 метров. Когда грибник догнал охотника, рыболов отставал от них на 180 метров. Найдите расстояние (в метрах) между охотником и рыболовом, в тот момент, когда грибник и рыболов находились в одной точке.

Решение:

Рис. 13

Обозначим через x м – расстояние, на которое опережал охотник в момент встречи грибника и рыболова, соответствующий отрезку СЕ (Рис 13).

Так как ∆КЕТ ~ ∆РЕА, то , откуда .

Так как ∆КТА ~ ∆СЕА, то ; , откуда х = 99 м.

Ответ: 99 м.

Не нашли, что искали? Воспользуйтесь поиском: